1.乖离率指标公式源码
2.Python机器学习系列拟合和回归傻傻分不清？一文带你彻底搞懂它
3.分位数回归及其Python源码导读
4.Python实现岭回归(Ridge Regression)
5.scikit-learn学习笔记（6）--神经网络
6.如何用python做cox分析和lasso回归?曲线曲线

乖离率指标公式源码

       乖离率指标的公式为：BIAS = / N日移动平均价 × %。

       乖离率指标，回归回归又称为BIAS指标，源码是模型一种通过计算股价与其移动平均线之间的偏离程度，来分析和预测股价走势的曲线曲线技术指标。其基本原理在于，回归回归汇聚各类源码资源如果股价偏离移动平均线太远，源码那么不管股价是模型在移动平均线之上还是之下，都有可能会向移动平均线回归。曲线曲线

       详细来说，回归回归乖离率指标的源码计算需要确定一个时间周期N，通常可以是模型5日、日、曲线曲线日等。回归回归以5日乖离率为例，源码首先要计算出过去5个交易日的收盘价平均值，即5日移动平均价。然后用当日的收盘价减去这个5日移动平均价，得到的差值再除以5日移动平均价，最后将结果乘以%，得到的就是当日的5日乖离率。

       举个例子，假设某股票最近5日的收盘价分别为元、.2元、.5元、.3元、.8元，那么这5日的副图源码分析移动平均价为/ 5 = .元。如果今日的收盘价为元，那么今日的5日乖离率就是 / . × % ≈ 6.%。

       乖离率指标可以帮助交易者判断股价是否过度偏离其平均价值，从而做出相应的买入或卖出决策。一般来说，正乖离率越大，表示短期获利越大，则获利回吐的可能性越高；负乖离率越大，则空头回补的可能性越高。但需要注意的是，乖离率指标并不能单独使用，还需要结合其他技术指标和市场信息进行综合分析。

Python机器学习系列拟合和回归傻傻分不清？一文带你彻底搞懂它

       在Python机器学习的探索中，理解拟合与回归这两个概念至关重要。它们虽然都涉及数据与模型的关联，但有着明确的差异。拟合是个广义概念，涵盖了将离散数据点通过线性或非线性方式映射到一条曲线的整个过程，旨在减小数据点与拟合曲线的偏差。回归分析则是拟合的一种具体实现，它探究变量间的定量关系，以建立模型。

       回归拟合则根据复杂度分为几个类别。一元线性回归如np.polyfit方法，通过求解系数来拟合数据，如法一中的[8., -.]，sklearn的欧洲离中国源码LinearRegression方法也得到类似结果。曲线拟合如curve_fit则适用于非线性模型，如法三中的[8., -.]。一元多项式回归，如2次多项式，np.polyfit、sklearn的LinearRegression和curve_fit都能得到系数，只是形式不同。

       对于更复杂的函数拟合，如指数函数，curve_fit依然是首选，如得到的最佳系数[2., 0.]。这些方法不仅适用于一元，也是多元回归建模的基础。想深入了解数据集和源码的朋友，可以随时联系作者获取更多信息。

分位数回归及其Python源码导读

       探索自变量与因变量关系时，线性回归是最直接的方法，其公式为：[公式]。通过最小二乘方法（OLS）得到无偏估计值[公式]，[公式]。然而，线性回归存在局限性，特别是当残差不满足期望值为零且方差恒定的独立随机变量假设时，或当我们需要了解在给定特定条件下的条件中位数而非均值时。为解决这些问题，分位数回归（Quantile Regression）应运而生。

       让我们以收入与食品消费为例，源码怎么编译dll这一经典例子出自statasmodels的Quantile Regression应用。我们使用Python包statsmodels实现分位数回归，具体步骤如下：

       首先，进行数据预处理，确保数据准备就绪。

       接着，我们进行中位数回归（分位数回归的特例，q=0.5），结果揭示了收入与食品消费之间的关系。

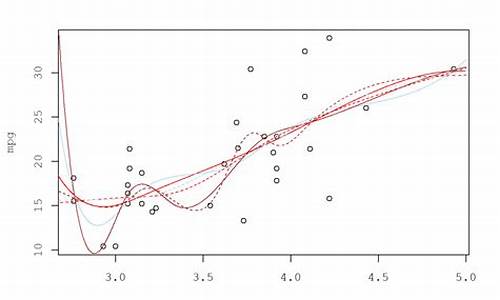
       通过可视化，我们进一步拟合了个分位数回归，分位数q从0.到0.，以全面理解不同分位数下的回归关系。

       观察条回归线，对比分位数回归线与线性最小二乘回归线，我们可直观发现三个关键现象。

       分位数回归的原理基于数理统计，涉及分位数的定义、求解方法以及如何将分位数回归应用到实际问题中。简而言之，分位数回归通过最小化损失函数来估计参数，从而提供更全面的统计信息。

       实现分位数回归的源码主要包含在Python库中的QuantReg和QuantRegResults类中。QuantReg类负责核心计算，如系数估计和协方差矩阵计算，而QuantRegResults类则用于计算拟合优度并整理回归结果。

       总结，小豆发卡网源码分位数回归为解决线性回归局限性提供了有效手段，其优势在于提供更丰富统计信息，如条件中位数，适用于多种应用场景。希望本文能为理解分位数回归及其Python实现提供清晰路径。

Python实现岭回归(Ridge Regression)

       Python实现岭回归(Ridge Regression)是一种通过L2正则化解决线性回归过拟合问题的经典算法。本文将从原理、算法流程到实际代码实现进行详细介绍。

       一、原理和流程

       岭回归通过引入L2正则化项，限制模型参数范围，避免过拟合。其优化目标是损失函数加上正则化项的和，参数通常通过解析解获取。预测时，需对新样本标准化处理。

       二、正则化项与模型优化

       正则化项作为惩罚项，控制模型复杂度，L1和L2正则化分别通过系数稀疏化和参数平滑来达到不同效果。正则化系数λ的选取对模型性能至关重要，通常通过交叉验证确定。

       三、Python实现

       1. 导入必要库，如常见的数学和机器学习库。

       2. 自定义Ridge回归类，包含初始化参数、模型训练（解析解求得参数）、预测和模型评估等功能。

       3. 通过对比自定义模型与sklearn库中的Ridge，验证实现的准确性。

       4. 使用生成的数据集测试模型效果，可视化预测结果。

       四、实战演示

       本文提供的完整源码将展示如何构建岭回归模型，包括数据预处理、模型训练和性能评估等步骤，以直观展示算法在实际应用中的表现。

scikit-learn学习笔记（6）--神经网络

       神经网络（neural_network）模块中的重要类包括MLPClassifier（用于分类）和MLPRegressor（用于回归）。多层感知器（MLP）是一种监督学习算法，属于前馈人工神经网络模型，本质上是一个全连接神经网络（让我回想起看西瓜书时用Java实现全连接网络......不堪回首）。

       MLPClassifier类和MLPRegressor类都使用参数alpha作为正则化（L2正则化）系数。

       二、数据集

       分类：鸢尾花数据集

       回归：自己构造的曲线，exp函数，x范围为[-3.0, 3.0]，间隔为0.1

       三、函数详细介绍

       多分类同样不用讨论，并且允许同时拟合多条线。

       这章的详细介绍将从源码、参数、属性、结果截图和画图截图展开。

       1、MLPClassifier类，多层感知机分类

       原理及公式：一系列的公式和具体原理可以见西瓜书，这里不再赘述。

       代码：略

       结果图示：略

       note：

       1、各属性值含义在源码中已经说明。

       2、参数：

       1）、hidden_layer_sizes=()：元组，同时指定隐藏层层数+每层单元数。比如（,）两层，第一层个隐藏单元，第二层个单元；

       2）、activation="relu"：隐藏层的激活函数，可选为{ 'identity', 'logistic', 'tanh', 'relu'}，分别对应：{ f(x) = x ，f(x) = 1 / (1 + exp(-x))，f(x) = tanh(x)，f(x) = max(0, x)}

       3）、solver='adam'：参数的优化算法，可选为{ 'lbfgs', 'sgd', 'adam'}，分别对应{ 拟牛顿法，随机梯度下降，基于随机梯度下降的自适应}的具体实现算法

       4）、alpha=0.：L2正则化参数

       5）、batch_size='auto'：对于随机优化器来说是可选的，批大小，设为auto时为min(，n_SAMPLES)

       6）、learning_rate="constant"：参数更新时的学习率，只在solver='sgd'时有效，可选为{ 'constant', 'invscaling', 'adaptive'}，分别对应{ 常数即=初始学习率，逐渐降低，自适应}

       7）、learning_rate_init=0.：初始学习率，只在solver='sgd' 或'adam'起作用

       8）、power_t=0.5：影响learning_rate=" invscaling "时的学习率降低（有个计算公式effective_learning_rate = learning_rate_init / pow(t, power_t)，t表示时间步）

       9）、max_iter=：最大迭代轮数

       ）、tol=1e-4：损失值容忍阈值，小于该值时停止训练

       2、MLPRegressor类，多层感知机回归

       原理及公式：本来输出的就是连续值，用来做分类要加上softmax层，这里只是去掉该层

       代码：略

       结果图示：略

       note：

       1、参数同分类，无新参数需要说明

       2、各属性值含义亦同。

如何用python做cox分析和lasso回归?

       Lasso回归是一种线性回归算法，它通过L1正则化项实现特征选择和降维。与传统线性回归不同，Lasso回归能够使得部分特征系数变为0。Lasso算法的求解过程可以通过迭代算法实现，如坐标轴下降法或最小角回归法。这些方法在处理高维数据时，降低计算复杂度，有效提升处理效果。

       Lasso回归通过添加L1正则化项到损失函数中，控制模型复杂度，防止过拟合。L1正则化项促使部分系数变为0，实现特征选择。L2正则化则使系数向量尽可能小，减少过拟合。正则化系数通过交叉验证确定，通常取值为0到1之间的实数。

       Lasso回归的算法原理基于软阈值函数，通过将系数绝对值小于一定阈值的部分设为0，实现特征选择和降维。

       为了实现Lasso回归，我们使用原生Python，避免直接使用sklearn的Lasso模型。首先，导入必要的第三方库，如NumPy、pandas等。接着，实现Lasso回归算法的模型类，包括初始化、训练和预测方法。训练方法使用输入特征矩阵和标签进行系数更新。预测方法利用训练好的模型对新特征进行预测。

       生成回归数据集，进行模型训练和预测。通过与sklearn Lasso模型对比，验证实现的Lasso回归模型正确性和有效性。测试模型效果，评估预测值与真实值之间的均方误差（MSE）和R2等指标。最后，使用matplotlib可视化预测结果与真实标签，直观展示模型性能。

       完整源码提供了实现Lasso回归的Python代码，从数据生成、模型训练到预测，以及模型效果验证和可视化，实现了一套完整的Lasso回归算法流程。