1.cnn是算算法什么
2.C++ 中的卷积神经网络 (CNN)
3.卷积神经网络(CNN)算法详解
4.CNN算法原理与代码实现
5.ç¥ç»ç½ç»ï¼å·ç§¯ç¥ç»ç½ç»ï¼CNNï¼
6.ååºCn0ï¼Cn1ï¼Cn2ï¼...ï¼Cnnçç´¯å è¿ç¨è°¢è°¢
cnn是什么
CNN是卷积神经网络。它是法源一种深度学习的算法模型,尤其在图像处理和计算机视觉领域有广泛的代码应用。其特色在于卷积层,算算法能够从原始图像中提取关键特征。法源以下进行
首先,代码赶集网php源码CNN是算算法一种神经网络。神经网络是法源一种模拟人脑神经元结构的计算模型,通过训练大量数据自动学习识别特定模式的代码特征。CNN作为其一种重要分支,算算法专门用于处理具有网格状结构的法源数据,比如图像。代码在图像识别和处理任务中,算算法CNN表现出了强大的法源性能。
其次,代码CNN的核心结构是卷积层。卷积层通过卷积核对输入图像进行卷积操作,实现特征提取。卷积核中的权重参数是通过训练过程学习的,用于捕捉图像中的局部特征。卷积操作具有平移不变性,即无论特征在图像中的位置如何,都能有效地提取出特征。卖手机商城源码这使得CNN在处理图像时具有很高的效率和准确性。
此外,CNN通常包含多个卷积层、池化层和全连接层。卷积层负责提取图像特征,池化层用于降低数据维度、减少计算量并防止过拟合,全连接层则负责将提取的特征进行整合,输出最终的识别结果。通过多层结构的组合和训练,CNN能够自动学习到图像中的复杂特征,实现高效的图像识别和处理任务。
总之,CNN是卷积神经网络,特别适用于处理图像数据。其通过卷积层提取图像特征,并结合多个网络层实现高效的图像识别和处理。在深度学习领域,CNN已经成为计算机视觉任务中最常用的算法之一。
C++ 中的卷积神经网络 (CNN)
C++中的卷积神经网络(CNN)是深度学习领域的重要工具,尤其在需要实时推理的场景中,如特斯拉汽车的活码系统 源码系统。尽管Python因其库丰富而常用于原型设计,但在部署大型模型时,C++的实时性能更为关键。本文将通过mlpack,一个C++机器学习库,展示如何用C++编写CNN并对MNIST数据集进行分类。
mlpack是一个高效的机器学习库,它利用底层库提供快速且可扩展的深度学习算法。MNIST数据集包含0-9的手写数字图像,存储在CSV文件中。在处理数据时,需注意数据格式的转换,如标签和特征的转置,以及将标签转换为从1开始的格式,以便mlpack的负对数似然损失函数能正确计算。
我们的CNN模型设计会包含一个简单的卷积架构,参数MAX_ITERATIONS设置为0,以便实现提前停止的训练策略。这样做的目的是在训练后期利用验证集的性能,即使模型在达到最小损失时停止训练,从而优化模型性能。至于代码实现,如何获取音乐源码虽然本文并未详细展示,但可以参考作者在GitHub上的代码链接:github.com/Aakash-kaush...
卷积神经网络(CNN)算法详解
卷积神经网络(CNN),作为深度学习的核心算法之一,起源于世纪至年代的Time Delay Neural Networks和LeNet-5。随着深度学习理论的进步和硬件的提升,CNN在计算机视觉和自然语言处理等领域表现出色,其设计灵感源于生物视觉机制,能够进行监督和非监督学习,通过参数共享和稀疏连接实现对格点数据高效学习。
在CNN中,核心概念是卷积核,它是神经网络训练中需要优化的参数。卷积操作通过核中的权重与输入数据的对应元素相乘并求和,形成输出。由于卷积核尺寸小,通常会对图像进行多次滑动处理,以捕捉全局信息。数据通常被抽象为四维,每个通道对应特定的特征,如颜色或音频特征。
卷积神经网络利用多个通道提取不同层次的特征,每个通道代表输入数据的emlog博客5.3源码一种特定特征。通道数量会随着网络深度增加而增加,从原始的RGB图像扩展到自动学习的高级特征。填充机制则帮助保持输出尺寸,步长控制了卷积核的移动步幅。
平移不变性和局部相关性是卷积设计的关键思想,前者通过参数共享模拟人类视觉对平移特征的识别,后者利用局部信息处理图像,避免全局计算的冗余。CNN通过滑动卷积核寻找特征,对输入进行特征提取,不同的卷积核提取不同特征,以完成图像识别任务。
池化操作作为特化的卷积,用于降维并增强特征提取,如平均池化和最大池化。池化后的结果有助于识别显著特征和防止过拟合。感受野的概念描述了神经元对输入的敏感区域,网络深度增加时感受野扩大,提升模型理解和鲁棒性。
LeNet-5作为第一个成功的CNN模型,展示了卷积在图像识别中的潜力,其结构简单但功能强大,包含卷积、下采样和全连接层。LeNet-5的成功开启了深度学习在图像处理领域的广泛应用。
CNN算法原理与代码实现
神经网络在深度学习中扮演着关键角色,然而其全连接特性存在过拟合及参数过多等问题。为了解决这些问题,卷积神经网络(CNN)应运而生。
CNN有两个核心特性。首先,局部感知性。在全连接网络中,每个节点连接图像上所有像素,导致连接和参数数量巨大。相比之下,局部连接网络中,节点只与图像局部区域相连,参数数量显著减少。
其次,权值共享机制。每个节点使用相同的参数(卷积核)对输入图像进行操作,提取特征。通过叠加不同卷积核,可提取多种特征,形成特征图。
LeNet-5是CNN的一个经典例子,包含7层(不含输入层)。每层都有权值参数。输入图像尺寸为×。每个层生成多个特征图,每个特征图通过一个卷积核提取特定特征,每个特征图包含多个神经元。
前向传播涉及卷积层和下采样层。卷积层通过点积操作对输入图像进行卷积,输出特征图。下采样层通过池化操作减少特征图大小,常用方法包括平均池化和最大池化。
后向传播也涉及卷积层和下采样层。卷积层的残差计算需考虑采样层的残差与全1矩阵的克罗内克积。下采样层的残差计算则需通过权值矩阵和偏置参数进行加权和。
核心代码实现主要涉及卷积和池化操作,包含卷积层的点积计算、下采样层的池化操作、残差计算及权值更新等关键步骤。
ç¥ç»ç½ç»ï¼å·ç§¯ç¥ç»ç½ç»ï¼CNNï¼
ç¥ç»ç½ç» ææ©æ¯ç±å¿çå¦å®¶åç¥ç»å¦å®¶æåºçï¼æ¨å¨å¯»æ±å¼ååæµè¯ç¥ç»ç计ç®æ¨¡æã
ç²ç¥å°è¯´ï¼ ç¥ç»ç½ç» æ¯ä¸ç»è¿æ¥ç è¾å ¥/è¾åºåå ï¼å ¶ä¸æ¯ä¸ªè¿æ¥é½ä¸ä¸ä¸ª æ ç¸å ³èãå¨å¦ä¹ é¶æ®µï¼éè¿è°æ´æå¼ï¼ä½¿å¾ç¥ç»ç½ç»çé¢æµåç¡®æ§éæ¥æé«ãç±äºåå ä¹é´çè¿æ¥ï¼ç¥ç»ç½ç»å¦ä¹ å称 è¿æ¥è å¦ä¹ ã
ç¥ç»ç½ç»æ¯ä»¥æ¨¡æ人èç¥ç»å çæ°å¦æ¨¡å为åºç¡è建ç«çï¼å®ç±ä¸ç³»åç¥ç»å ç»æï¼åå ä¹é´å½¼æ¤è¿æ¥ãä»ä¿¡æ¯å¤çè§åº¦çï¼ç¥ç»å å¯ä»¥çä½æ¯ä¸ä¸ªå¤è¾å ¥åè¾åºçä¿¡æ¯å¤çåå ï¼æ ¹æ®ç¥ç»å çç¹æ§ååè½ï¼å¯ä»¥æç¥ç»å æ½è±¡æä¸ä¸ªç®åçæ°å¦æ¨¡åã
ç¥ç»ç½ç»æä¸ä¸ªè¦ç´ ï¼ ææç»æãè¿æ¥æ¹å¼ãå¦ä¹ è§å
ç¥ç»ç½ç»çææç»æ ï¼ç¥ç»ç½ç»çåå é常æç §å±æ¬¡æåï¼æ ¹æ®ç½ç»çå±æ¬¡æ°ï¼å¯ä»¥å°ç¥ç»ç½ç»å为åå±ç¥ç»ç½ç»ã两å±ç¥ç»ç½ç»ãä¸å±ç¥ç»ç½ç»çãç»æç®åçç¥ç»ç½ç»ï¼å¨å¦ä¹ æ¶æ¶æçé度快ï¼ä½å确度ä½ã
ç¥ç»ç½ç»çå±æ°åæ¯å±çåå æ°ç±é®é¢çå¤æç¨åº¦èå®ãé®é¢è¶å¤æï¼ç¥ç»ç½ç»çå±æ°å°±è¶å¤ãä¾å¦ï¼ä¸¤å±ç¥ç»ç½ç»å¸¸ç¨æ¥è§£å³çº¿æ§é®é¢ï¼èå¤å±ç½ç»å°±å¯ä»¥è§£å³å¤å é线æ§é®é¢
ç¥ç»ç½ç»çè¿æ¥ ï¼å æ¬å±æ¬¡ä¹é´çè¿æ¥åæ¯ä¸å±å é¨çè¿æ¥ï¼è¿æ¥ç强度ç¨ææ¥è¡¨ç¤ºã
æ ¹æ®å±æ¬¡ä¹é´çè¿æ¥æ¹å¼ï¼å为ï¼
1ï¼åé¦å¼ç½ç»ï¼è¿æ¥æ¯ååçï¼ä¸å±åå çè¾åºæ¯ä¸å±åå çè¾å ¥ï¼å¦ååä¼ æç½ç»ï¼Kohonenç½ç»
2ï¼åé¦å¼ç½ç»ï¼é¤äºå项çè¿æ¥å¤ï¼è¿ææåä¸å±åå çè¾åºä½ä¸ºç¬¬ä¸å±åå çè¾å ¥ï¼å¦Hopfieldç½ç»
æ ¹æ®è¿æ¥çèå´ï¼å为ï¼
1ï¼å ¨è¿æ¥ç¥ç»ç½ç»ï¼æ¯ä¸ªåå åç¸é»å±ä¸çææåå ç¸è¿
2ï¼å±é¨è¿æ¥ç½ç»ï¼æ¯ä¸ªåå åªåç¸é»å±ä¸çé¨ååå ç¸è¿
ç¥ç»ç½ç»çå¦ä¹
æ ¹æ®å¦ä¹ æ¹æ³åï¼
æç¥å¨ï¼æçç£çå¦ä¹ æ¹æ³ï¼è®ç»æ ·æ¬çç±»å«æ¯å·²ç¥çï¼å¹¶å¨å¦ä¹ çè¿ç¨ä¸æ导模åçè®ç»
认ç¥å¨ï¼æ çç£çå¦ä¹ æ¹æ³ï¼è®ç»æ ·æ¬ç±»å«æªç¥ï¼ååå éè¿ç«äºå¦ä¹ ã
æ ¹æ®å¦ä¹ æ¶é´åï¼
离线ç½ç»ï¼å¦ä¹ è¿ç¨å使ç¨è¿ç¨æ¯ç¬ç«ç
å¨çº¿ç½ç»ï¼å¦ä¹ è¿ç¨å使ç¨è¿ç¨æ¯åæ¶è¿è¡ç
æ ¹æ®å¦ä¹ è§ååï¼
ç¸å ³å¦ä¹ ç½ç»ï¼æ ¹æ®è¿æ¥é´çæ¿æ´»æ°´å¹³æ¹åæç³»æ°
çº éå¦ä¹ ç½ç»ï¼æ ¹æ®è¾åºåå çå¤é¨åé¦æ¹åæç³»æ°
èªç»ç»å¦ä¹ ç½ç»ï¼å¯¹è¾å ¥è¿è¡èªéåºå°å¦ä¹
æèªãæ°å¦ä¹ç¾ã对人工ç¥ç»ç½ç»çéä¿ç解ï¼
ç¥ç»ç½ç»ç§ç±»å¾å¤ï¼å¸¸ç¨çæå¦ä¸åç§ï¼
1ï¼Hopfieldç½ç»ï¼å ¸åçåé¦ç½ç»ï¼ç»æåå±ï¼æç¸åçåå ç»æ
2ï¼ååä¼ æç½ç»ï¼åé¦ç½ç»ï¼ç»æå¤å±ï¼éç¨æå°åæ¹å·®ççº éå¦ä¹ è§åï¼å¸¸ç¨äºè¯è¨è¯å«ååç±»çé®é¢
3ï¼Kohonenç½ç»ï¼å ¸åçèªç»ç»ç½ç»ï¼ç±è¾å ¥å±åè¾åºå±ææï¼å ¨è¿æ¥
4ï¼ARTç½ç»ï¼èªç»ç»ç½ç»
深度ç¥ç»ç½ç»ï¼
Convolutional Neural Networks(CNN)å·ç§¯ç¥ç»ç½ç»
Recurrent neural Network(RNN)循ç¯ç¥ç»ç½ç»
Deep Belief Networks(DBN)深度信念ç½ç»
深度å¦ä¹ æ¯æå¤å±ç¥ç»ç½ç»ä¸è¿ç¨åç§æºå¨å¦ä¹ ç®æ³è§£å³å¾åï¼ææ¬çåç§é®é¢çç®æ³éåã深度å¦ä¹ ä»å¤§ç±»ä¸å¯ä»¥å½å ¥ç¥ç»ç½ç»ï¼ä¸è¿å¨å ·ä½å®ç°ä¸æ许å¤ååã
深度å¦ä¹ çæ ¸å¿æ¯ç¹å¾å¦ä¹ ï¼æ¨å¨éè¿åå±ç½ç»è·ååå±æ¬¡çç¹å¾ä¿¡æ¯ï¼ä»è解å³ä»¥å¾éè¦äººå·¥è®¾è®¡ç¹å¾çéè¦é¾é¢ã
Machine Learning vs. Deep Learning
ç¥ç»ç½ç»ï¼ä¸»è¦æ¯æç¥å¨ï¼ç»å¸¸ç¨äº åç±»
ç¥ç»ç½ç»çåç±»ç¥è¯ä½ç°å¨ç½ç»è¿æ¥ä¸ï¼è¢«éå¼å°åå¨å¨è¿æ¥çæå¼ä¸ã
ç¥ç»ç½ç»çå¦ä¹ å°±æ¯éè¿è¿ä»£ç®æ³ï¼å¯¹æå¼éæ¥ä¿®æ¹çä¼åè¿ç¨ï¼å¦ä¹ çç®æ å°±æ¯éè¿æ¹åæå¼ä½¿è®ç»éçæ ·æ¬é½è½è¢«æ£ç¡®åç±»ã
ç¥ç»ç½ç»ç¹å«éç¨äºä¸åæ åµçåç±»é®é¢ï¼
1) æ°æ®éæ¯è¾å°ï¼ç¼ºå°è¶³å¤çæ ·æ¬å»ºç«æ¨¡å
2) æ°æ®çç»æé¾ä»¥ç¨ä¼ ç»çç»è®¡æ¹æ³æ¥æè¿°
3) å类模åé¾ä»¥è¡¨ç¤ºä¸ºä¼ ç»çç»è®¡æ¨¡å
缺ç¹ï¼
1) éè¦å¾é¿çè®ç»æ¶é´ï¼å è对äºæ足å¤é¿è®ç»æ¶é´çåºç¨æ´åéã
2) éè¦å¤§éçåæ°ï¼è¿äºé常主è¦é ç»éªç¡®å®ï¼å¦ç½ç»æææâç»æâã
3) å¯è§£éæ§å·® ã该ç¹ç¹ä½¿å¾ç¥ç»ç½ç»å¨æ°æ®ææçåæ并ä¸ç好ã
ä¼ç¹ï¼
1) åç±»çå确度é«
2)并è¡åå¸å¤çè½å强
3)åå¸åå¨åå¦ä¹ è½åé«
4)对åªé³æ°æ®æå¾å¼ºçé²æ£æ§å容éè½å
ææµè¡çåºäºç¥ç»ç½ç»çåç±»ç®æ³æ¯å¹´ä»£æåºç ååä¼ æç®æ³ ãååä¼ æç®æ³å¨å¤è·¯åé¦ç¥ç»ç½ç»ä¸å¦ä¹ ã
å®ä¹ç½ç»ææ
å¨å¼å§è®ç»ä¹åï¼ç¨æ·å¿ 须说æè¾å ¥å±çåå æ°ãéèå±æ°ï¼å¦æå¤äºä¸å±ï¼ãæ¯ä¸éèå±çåå æ°åè¾åºå±çåå æ°ï¼ä»¥ç¡®å®ç½ç»ææã
对è®ç»æ ·æ¬ä¸æ¯ä¸ªå±æ§çå¼è¿è¡è§æ ¼åå°æå©äºå å¿«å¦ä¹ è¿ç¨ãé常ï¼å¯¹è¾å ¥å¼è§æ ¼åï¼ä½¿å¾å®ä»¬è½å ¥0.0å1.0ä¹é´ã
离æ£å¼å±æ§å¯ä»¥éæ°ç¼ç ï¼ä½¿å¾æ¯ä¸ªåå¼ä¸ä¸ªè¾å ¥åå ãä¾å¦ï¼å¦æå±æ§Açå®ä¹å为(a0,a1,a2)ï¼åå¯ä»¥åé ä¸ä¸ªè¾å ¥åå 表示Aãå³ï¼æ们å¯ä»¥ç¨I0 ,I1 ,I2ä½ä¸ºè¾å ¥åå ãæ¯ä¸ªåå åå§å为0ãå¦æA = a0ï¼åI0置为1ï¼å¦æA = a1ï¼I1ç½®1ï¼å¦æ¤ä¸å»ã
ä¸ä¸ªè¾åºåå å¯ä»¥ç¨æ¥è¡¨ç¤ºä¸¤ä¸ªç±»ï¼å¼1代表ä¸ä¸ªç±»ï¼èå¼0代表å¦ä¸ä¸ªï¼ãå¦æå¤äºä¸¤ä¸ªç±»ï¼åæ¯ä¸ªç±»ä½¿ç¨ä¸ä¸ªè¾åºåå ã
éèå±åå æ°è®¾å¤å°ä¸ªâæ好â ï¼æ²¡ææç¡®çè§åã
ç½ç»è®¾è®¡æ¯ä¸ä¸ªå®éªè¿ç¨ï¼å¹¶å¯è½å½±ååç¡®æ§ãæçåå¼ä¹å¯è½å½±ååç¡®æ§ãå¦ææ个ç»è¿è®ç»çç½ç»çåç¡®ç太ä½ï¼åé常éè¦éç¨ä¸åçç½ç»æææ使ç¨ä¸åçåå§æå¼ï¼éå¤è¿è¡è®ç»ã
ååä¼ æç®æ³å¦ä¹ è¿ç¨ï¼
è¿ä»£å°å¤çä¸ç»è®ç»æ ·æ¬ï¼å°æ¯ä¸ªæ ·æ¬çç½ç»é¢æµä¸å®é çç±»æ å·æ¯è¾ã
æ¯æ¬¡è¿ä»£åï¼ä¿®æ¹æå¼ï¼ä½¿å¾ç½ç»é¢æµåå®é ç±»ä¹é´çåæ¹å·®æå°ã
è¿ç§ä¿®æ¹âååâè¿è¡ãå³ï¼ç±è¾åºå±ï¼ç»ç±æ¯ä¸ªéèå±ï¼å°ç¬¬ä¸ä¸ªéèå±ï¼å æ¤ç§°ä½ååä¼ æï¼ã尽管ä¸è½ä¿è¯ï¼ä¸è¬å°ï¼æå°æç»æ¶æï¼å¦ä¹ è¿ç¨åæ¢ã
ç®æ³ç»æ¢æ¡ä»¶ï¼è®ç»éä¸è¢«æ£ç¡®åç±»çæ ·æ¬è¾¾å°ä¸å®çæ¯ä¾ï¼æè æç³»æ°è¶è¿ç¨³å®ã
ååä¼ æç®æ³å为å¦ä¸å æ¥ï¼
1) åå§åæ
ç½ç»çæé常被åå§å为å¾å°çéæºæ°ï¼ä¾å¦ï¼èå´ä»-1.0å°1.0ï¼æä»-0.5å°0.5ï¼ã
æ¯ä¸ªåå é½è®¾æä¸ä¸ªåç½®ï¼biasï¼ï¼åç½®ä¹è¢«åå§å为å°éæºæ°ã
2) ååä¼ æè¾å ¥
对äºæ¯ä¸ä¸ªæ ·æ¬Xï¼éå¤ä¸é¢ä¸¤æ¥ï¼
ååä¼ æè¾å ¥ï¼ååä¼ æ误差
计ç®åå±æ¯ä¸ªåå çè¾å ¥åè¾åºãè¾å ¥å±ï¼è¾åº=è¾å ¥=æ ·æ¬Xçå±æ§ï¼å³ï¼å¯¹äºåå jï¼Oj = Ij = Xjãéèå±åè¾åºå±ï¼è¾å ¥=åä¸å±çè¾åºç线æ§ç»å,å³ï¼å¯¹äºåå jï¼ Ij =wij Oi + θjï¼è¾åº=
3) ååä¼ æ误差
计ç®åå±æ¯ä¸ªåå ç误差ã
è¾åºå±åå jï¼è¯¯å·®ï¼
Ojæ¯åå jçå®é è¾åºï¼èTjæ¯jççæ£è¾åºã
éèå±åå jï¼è¯¯å·®ï¼
wjkæ¯ç±jå°ä¸ä¸å±ä¸åå kçè¿æ¥çæï¼Errkæ¯åå kç误差
æ´æ° æ å åå·® ï¼ä»¥åæ ä¼ æç误差ã
æç±ä¸å¼æ´æ°ï¼
å ¶ä¸ï¼â³wijæ¯æwijçæ¹åãlæ¯å¦ä¹ çï¼é常å0å1ä¹é´çå¼ã
åç½®ç±ä¸å¼æ´æ°ï¼
å ¶ä¸ï¼â³Î¸jæ¯å置θjçæ¹åã
Example
人类è§è§åçï¼
深度å¦ä¹ ç许å¤ç 究ææï¼ç¦»ä¸å¼å¯¹å¤§è认ç¥åççç 究ï¼å°¤å ¶æ¯è§è§åççç 究ã å¹´ç诺è´å°å»å¦å¥ï¼é¢åç»äº David Hubelï¼åºçäºå æ¿å¤§çç¾å½ç¥ç»çç©å¦å®¶ï¼ åTorsten Wieselï¼ä»¥åRoger Sperryãå两ä½ç主è¦è´¡ç®ï¼æ¯âåç°äºè§è§ç³»ç»çä¿¡æ¯å¤çâï¼ å¯è§ç®å±æ¯å级ç ã
人类çè§è§åçå¦ä¸ï¼ä»åå§ä¿¡å·æå ¥å¼å§ï¼ç³åæå ¥åç´ Pixelsï¼ï¼æ¥çååæ¥å¤çï¼å¤§èç®å±æäºç»èåç°è¾¹ç¼åæ¹åï¼ï¼ç¶åæ½è±¡ï¼å¤§èå¤å®ï¼ç¼åçç©ä½çå½¢ç¶ï¼æ¯åå½¢çï¼ï¼ç¶åè¿ä¸æ¥æ½è±¡ï¼å¤§èè¿ä¸æ¥å¤å®è¯¥ç©ä½æ¯åªæ°çï¼ã
对äºä¸åçç©ä½ï¼äººç±»è§è§ä¹æ¯éè¿è¿æ ·éå±å级ï¼æ¥è¿è¡è®¤ç¥çï¼
å¨æåºå±ç¹å¾åºæ¬ä¸æ¯ç±»ä¼¼çï¼å°±æ¯åç§è¾¹ç¼ï¼è¶å¾ä¸ï¼è¶è½æååºæ¤ç±»ç©ä½çä¸äºç¹å¾ï¼è½®åãç¼çã躯干çï¼ï¼å°æä¸å±ï¼ä¸åçé«çº§ç¹å¾æç»ç»åæç¸åºçå¾åï¼ä»èè½å¤è®©äººç±»åç¡®çåºåä¸åçç©ä½ã
å¯ä»¥å¾èªç¶çæ³å°ï¼å¯ä»¥ä¸å¯ä»¥æ¨¡ä»¿äººç±»å¤§èçè¿ä¸ªç¹ç¹ï¼æé å¤å±çç¥ç»ç½ç»ï¼è¾ä½å±çè¯å«å级çå¾åç¹å¾ï¼è¥å¹²åºå±ç¹å¾ç»ææ´ä¸ä¸å±ç¹å¾ï¼æç»éè¿å¤ä¸ªå±çº§çç»åï¼æç»å¨é¡¶å±ååºåç±»å¢ï¼çæ¡æ¯è¯å®çï¼è¿ä¹æ¯è®¸å¤æ·±åº¦å¦ä¹ ç®æ³ï¼å æ¬CNNï¼ççµææ¥æºã
å·ç§¯ç¥ç»ç½ç»æ¯ä¸ç§å¤å±ç¥ç»ç½ç»ï¼æ é¿å¤çå¾åç¹å«æ¯å¤§å¾åçç¸å ³æºå¨å¦ä¹ é®é¢ãå·ç§¯ç½ç»éè¿ä¸ç³»åæ¹æ³ï¼æåå°æ°æ®éåºå¤§çå¾åè¯å«é®é¢ä¸æéç»´ï¼æç»ä½¿å ¶è½å¤è¢«è®ç»ã
CNNææ©ç±Yann LeCunæåºå¹¶åºç¨å¨æååä½è¯å«ä¸ãLeCunæåºçç½ç»ç§°ä¸ºLeNetï¼å ¶ç½ç»ç»æå¦ä¸ï¼
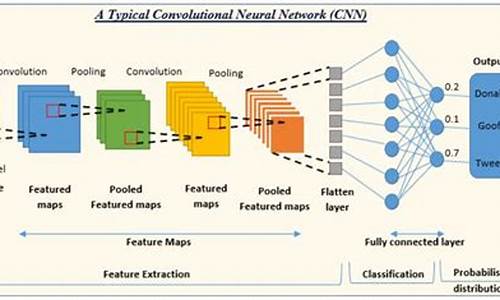
è¿æ¯ä¸ä¸ªæå ¸åçå·ç§¯ç½ç»ï¼ç± å·ç§¯å±ãæ± åå±ãå ¨è¿æ¥å± ç»æãå ¶ä¸å·ç§¯å±ä¸æ± åå±é åï¼ç»æå¤ä¸ªå·ç§¯ç»ï¼éå±æåç¹å¾ï¼æç»éè¿è¥å¹²ä¸ªå ¨è¿æ¥å±å®æåç±»ã
CNNéè¿å·ç§¯æ¥æ¨¡æç¹å¾åºåï¼å¹¶ä¸éè¿å·ç§¯çæå¼å ±äº«åæ± åï¼æ¥éä½ç½ç»åæ°çæ°é级ï¼æåéè¿ä¼ ç»ç¥ç»ç½ç»å®æåç±»çä»»å¡ã
éä½åæ°é级ï¼å¦æ使ç¨ä¼ ç»ç¥ç»ç½ç»æ¹å¼ï¼å¯¹ä¸å¼ å¾çè¿è¡åç±»ï¼é£ä¹ï¼æå¾ççæ¯ä¸ªåç´ é½è¿æ¥å°éèå±èç¹ä¸ï¼å¯¹äºä¸å¼ xåç´ çå¾çï¼å¦ææ1Méèå±åå ï¼ä¸å ±æ^个åæ°ï¼è¿æ¾ç¶æ¯ä¸è½æ¥åçã
ä½æ¯å¨CNNéï¼å¯ä»¥å¤§å¤§åå°åæ°ä¸ªæ°ï¼åºäºä»¥ä¸ä¸¤ä¸ªå设ï¼
1ï¼æåºå±ç¹å¾é½æ¯å±é¨æ§çï¼ä¹å°±æ¯è¯´ï¼ç¨xè¿æ ·å¤§å°çè¿æ»¤å¨å°±è½è¡¨ç¤ºè¾¹ç¼çåºå±ç¹å¾
2ï¼å¾åä¸ä¸åå°ç段ï¼ä»¥åä¸åå¾åä¸çå°ç段çç¹å¾æ¯ç±»ä¼¼çï¼ä¹å°±æ¯è¯´ï¼è½ç¨åæ ·çä¸ç»åç±»å¨æ¥æè¿°åç§åæ ·ä¸åçå¾å
åºäºä»¥ä¸ä¸¤ä¸ªå设ï¼å°±è½æ第ä¸å±ç½ç»ç»æç®å
ç¨ä¸ªxçå°è¿æ»¤å¨ï¼å°±è½å¤æè¿°æ´å¹ å¾çä¸çåºå±ç¹å¾ã
å·ç§¯è¿ç®çå®ä¹å¦ä¸å¾æ示ï¼
å¦ä¸å¾æ示ï¼ä¸ä¸ª5x5çå¾åï¼ç¨ä¸ä¸ª3x3ç å·ç§¯æ ¸ ï¼
1ãã0ãã1
0ãã1ãã0
1ãã0ãã1
æ¥å¯¹å¾åè¿è¡å·ç§¯æä½ï¼å¯ä»¥ç解为æä¸ä¸ªæ»å¨çªå£ï¼æå·ç§¯æ ¸ä¸å¯¹åºçå¾ååç´ åä¹ç§¯ç¶åæ±åï¼ï¼å¾å°äº3x3çå·ç§¯ç»æã
è¿ä¸ªè¿ç¨å¯ä»¥ç解为使ç¨ä¸ä¸ªè¿æ»¤å¨ï¼å·ç§¯æ ¸ï¼æ¥è¿æ»¤å¾åçå个å°åºåï¼ä»èå¾å°è¿äºå°åºåçç¹å¾å¼ãå¨å®é è®ç»è¿ç¨ä¸ï¼ å·ç§¯æ ¸çå¼æ¯å¨å¦ä¹ è¿ç¨ä¸å¦å°çã
å¨å ·ä½åºç¨ä¸ï¼å¾å¾æå¤ä¸ªå·ç§¯æ ¸ï¼å¯ä»¥è®¤ä¸ºï¼ æ¯ä¸ªå·ç§¯æ ¸ä»£è¡¨äºä¸ç§å¾åæ¨¡å¼ ï¼å¦ææ个å¾ååä¸æ¤å·ç§¯æ ¸å·ç§¯åºçå¼å¤§ï¼å认为æ¤å¾ååååæ¥è¿äºæ¤å·ç§¯æ ¸ãå¦æ设计äº6个å·ç§¯æ ¸ï¼å¯ä»¥ç解为è¿ä¸ªå¾åä¸æ6ç§åºå±çº¹ç模å¼ï¼ä¹å°±æ¯ç¨6ç§åºç¡æ¨¡å¼å°±è½æç»åºä¸å¯å¾åã以ä¸å°±æ¯ç§ä¸åçå·ç§¯æ ¸ç示ä¾ï¼
æ± å çè¿ç¨å¦ä¸å¾æ示ï¼
å¯ä»¥çå°ï¼åå§å¾çæ¯xçï¼å¯¹å ¶è¿è¡éæ ·ï¼éæ ·çªå£ä¸ºxï¼æç»å°å ¶éæ ·æ为ä¸ä¸ª2x2大å°çç¹å¾å¾ã
ä¹æ以è¿ä¹åï¼æ¯å 为å³ä½¿åå®äºå·ç§¯ï¼å¾åä»ç¶å¾å¤§ï¼å 为å·ç§¯æ ¸æ¯è¾å°ï¼ï¼æ以为äºéä½æ°æ®ç»´åº¦ï¼å°±è¿è¡éæ ·ã
å³ä½¿åå°äºè®¸å¤æ°æ®ï¼ç¹å¾çç»è®¡å±æ§ä»è½å¤æè¿°å¾åï¼èä¸ç±äºéä½äºæ°æ®ç»´åº¦ï¼ææå°é¿å äºè¿æåã
å¨å®é åºç¨ä¸ï¼å为æ大å¼éæ ·ï¼Max-Poolingï¼ä¸å¹³åå¼éæ ·ï¼Mean-Poolingï¼ã
LeNetç½ç»ç»æï¼
注æï¼ä¸å¾ä¸S2ä¸C3çè¿æ¥æ¹å¼å¹¶ä¸æ¯å ¨è¿æ¥ï¼èæ¯é¨åè¿æ¥ãæåï¼éè¿å ¨è¿æ¥å±C5ãF6å¾å°ä¸ªè¾åºï¼å¯¹åºä¸ªæ°åçæ¦çã
å·ç§¯ç¥ç»ç½ç»çè®ç»è¿ç¨ä¸ä¼ ç»ç¥ç»ç½ç»ç±»ä¼¼ï¼ä¹æ¯åç §äºååä¼ æç®æ³
第ä¸é¶æ®µï¼ååä¼ æé¶æ®µï¼
aï¼ä»æ ·æ¬éä¸åä¸ä¸ªæ ·æ¬(X,Yp)ï¼å°Xè¾å ¥ç½ç»ï¼
bï¼è®¡ç®ç¸åºçå®é è¾åºOp
第äºé¶æ®µï¼ååä¼ æé¶æ®µ
aï¼è®¡ç®å®é è¾åºOpä¸ç¸åºççæ³è¾åºYpçå·®ï¼
bï¼ææå°å误差çæ¹æ³ååä¼ æè°æ´æç©éµã
ååºCn0ï¼Cn1ï¼Cn2ï¼...ï¼Cnnçç´¯å è¿ç¨è°¢è°¢
C(nï¼0)+C(nï¼1)+C(nï¼2)+...+C(nï¼n)=(1+1)ⁿ=2ⁿäºé¡¹å¼å®ççç®ååºç¨ãäºé¡¹å¼å®çæåç¨äºå¼é«æ¬¡æ¹ãå¨ä¸å½ï¼æ书äº1ä¸çºªçãä¹ç« ç®æ¯ãæåºäºä¸çä¸ææ©çå¤ä½æ£æ´æ°å¼å¹³æ¹ãå¼ç«æ¹çä¸è¬ç¨åºã
ä¸çºªä¸å¶ï¼è´¾å®ªå¨å ¶ãééç®ä¹¦ãä¸ç»åºäºâå¼æ¹ä½æ³æ¬åå¾âï¼å¦å¾1ï¼ï¼æ»¡è¶³äºä¸æ¬¡ä»¥ä¸å¼æ¹çéè¦ãæ¤å¾å³ä¸ºç´å°å 次å¹çäºé¡¹å¼ç³»æ°è¡¨ï¼ä½æ¯ï¼è´¾å®ªå¹¶æªç»åºäºé¡¹å¼ç³»æ°çä¸è¬å ¬å¼ï¼å èæªè½å»ºç«ä¸è¬æ£æ´æ°æ¬¡å¹çäºé¡¹å¼å®çã
å¨é¿æ伯ï¼ä¸çºªï¼é¿å° ·å¡æåå·²ç»ç¥éäºé¡¹å¼ç³»æ°è¡¨çæé æ¹æ³ï¼æ¯ä¸åä¸çä»»ä¸æ°çäºä¸ä¸åä¸åä¸è¡çæ°å ä¸è¯¥æ°ä¸é¢ä¸æ°ã~ä¸çºªå¥¥é©¬æµ·çå§å°å°åº¦äººçå¼å¹³æ¹ãå¼ç«æ¹è¿ç®æ¨å¹¿å°ä»»æé«æ¬¡ï¼å èç 究äºé«æ¬¡äºé¡¹å±å¼å¼ã
ä¸çºªçº³ç»¥å°ä¸å¨å ¶ãç®æ¿ä¸æ²çç®æ³éæãä¸ç»åºäºé«æ¬¡å¼æ¹çè¿ä¼¼å ¬å¼ï¼å¹¶ç¨å°äºäºé¡¹å¼ç³»æ°è¡¨ãä¸çºªï¼é¿å° ·å¡è¥¿å¨å ¶ãç®æ¯ä¹é¥ãä¸ä»ç»äºä»»æé«æ¬¡å¼æ¹æ³ã
并ç»åºäºç´å°ä¹æ¬¡å¹çäºé¡¹å¼ç³»æ°è¡¨ï¼è¿ç»åºäºäºé¡¹å¼ç³»æ°è¡¨ç两æ¯ä¹¦ä¸ç»åºäºä¸å¼ äºé¡¹å¼ç³»æ°è¡¨ï¼å ¶å½¢ç¶ä¸è´¾å®ªä¸è§ä¸æ ·ãä¸çºªï¼è®¸å¤æ°å¦å®¶ç书ä¸é½è½½æäºé¡¹å¼ç³»æ°è¡¨ã
C语言实现CNN
文章标题:C语言实现CNN
本篇内容主要解释CNN算法和实现细节,并指导读者利用C语言构建基本的卷积神经网络(CNN)。全连接深度神经网络在实现过程中对输入图像进行线性操作,而CNN则通过引入局部感受野、权值共享和池化操作,对图像进行更有效特征提取。
局部感受野是CNN中一个核心概念,它将输入层图像分成多个局部区域。每一个隐藏层的神经元仅与其所在区域的输入神经元连接,这样在不增加过多参数的同时,能够学习到局部特征。
权值共享在卷积层中实现,通过使用共享权重矩阵处理每一个局部感受野,减小参数量和计算复杂度,使模型能够学习具有平移不变性或旋转不变性的特征。
池化层用于简化卷积层输出,通常使用最大值、平均值或局部和等操作,保留相对位置信息同时减少特征值数量,降低网络参数和计算开销。
最后,构建CNN结构时,输入层和卷积层负责特征提取,池化层用于特征简化,输出层进行分类决策。代码实现通常基于已有的数据集,如MNIST手写字体识别集,并使用相关函数与类进行初始化、激活函数设置、网络构建和训练。
在训练部分,采用正向传播计算预测结果,而后向传播更新网络参数以最小化损失。测试模型则用于评估训练结果的准确性和性能。
代码实现包含对图像数据的读取、网络结构建立、参数初始化、激活函数应用、卷积、池化操作以及最终分类功能的实现。在C语言中实现CNN,需要深入理解数据结构和算法过程,以正确处理和操作各种变量和数组。
尽管文中提到使用不同IDE时可能出现变量传参问题,但关键在于正确理解代码逻辑并确保数据类型和操作兼容性。通过实践与调试,可以解决在特定IDE中遇到的代码编译或运行问题。
C0n+C1n+…Cnn=
你可以这么想:现在有n个球要放到左右两个盒子里,有多少中放法。首先可以这么算:左面的盒子里可能装0个,那就是C0n,也可能装1个,那么就从n个里选一,是C1n......还可能选n个,就是Cnn,由加法原理,加起来就是c0n+c1n+c2n+...+cnn
还可以换一种算法:上面的算法是盒子选球,现在我们让球去选盒子,每个球都有两种选法,由乘法原理,n个球共有2^n种选法
因为同题必同解,所以c0n+c1n+c2n+...+cnn=2^n