1.计算机中的源码乘原代码、补码、源码乘逆码怎么表示？
2.原码二位乘法100为什么是源码乘加2x？
3.C语言编程九九乘法表
4.HDL系列乘法器(2)——阵列乘法器

计算机中的原代码、补码、源码乘逆码怎么表示？

       一、源码乘小数部分的源码乘易遨mse源码原码和补码可以表示为两个复数的分子和分母，然后计算二进制小数系统，源码乘根据下面三步的源码乘方法就会找出小数源代码和补码的百位形式。

       ／＝B／2＾6＝0．B

       －／＝B／2＾7＝0．B

       二、源码乘将十进制十进制原始码和补码转换成二进制十进制，源码乘然后根据下面三步的源码乘方法求出十进制源代码和补码形式。一个

       0．＝0．B

       0．＝0．B

       三、源码乘二进制十进制对应的源码乘原码和补码

       ［／］源代码＝［0．B］源代码＝B

       ［－／］源代码＝［0．b］源代码＝B

       ［0．］原码＝［0．b］原码＝B

       ［0．］源代码＝［0．B］源代码＝B

       ［／］补体＝［0．B］补体＝B

       ［－／］补体＝［0．b］补体＝B

       ［0．］补码＝［0．b］补码＝B

       ［0．］补体＝［0．B］补体＝B

扩展资料：

       原码、逆码、源码乘补码的源码乘使用：

       在计算机中对数字编码有三种方法，对于正数，中兴rosng源码这三种方法返回的结果是相同的。

       ＋1＝［原码］＝［逆码］＝［补码］

       对于这个负数：

       对计算机来说，加、减、乘、除是最基本的运算。有必要使设计尽可能简单。如果计算机能够区分符号位，那么计算机的基本电路设计就会变得更加复杂。

       负的正数等于正的负数，2－1等于2＋（－1）所以这个机器只做加法，不做减法。符号位参与运算，只保留加法运算。

       （1）原始代码操作：

       十进制操作：1－1＝0。编译vscode源码

       1－1＝1＋（－1）＝［源代码］＋［源代码］＝［源代码］＝－2。

       如果用原代码来表示，让符号位也参与计算，对于减法，结果显然是不正确的，所以计算机不使用原代码来表示一个数字。

       （2）逆码运算：

       为了解决原码相减的问题，引入了逆码。

       十进制操作：1－1＝0。

       1－1＝1＋（－1）＝［源代码］＋［源代码］＝［源代码］＋［源代码］＝［源代码］＝［源代码］＝－0。

       使用反减法，结果的真值部分是正确的，但在特定的值“0”。虽然＋0和－0在某种意义上是相同的，但是手表手机源码0加上符号是没有意义的，［源代码］和［源代码］都代表0。

       （3）补充操作：

       补语的出现解决了零和两个码的符号问题。

       十进制运算：1－1＝0。

       1－1＝1＋（－1）＝［原码］＋［原码］＝［补码］＋［补码］＝［补码］＝［原码］＝0。

       这样，0表示为［］，而之前的－0问题不存在，可以表示为［］－。

       （－1）＋（－）＝［源代码］＋［源代码］＝［补充］＋［补充］＝［补充］＝－。

       －1－的结果应该是－。在补码操作的结果中，［补码］是－，但是请注意，由于－0的补码实际上是用来表示－的，所以－没有原码和逆码。java源码abcd（－的补码表［补码］计算出的［原码］是不正确的）。

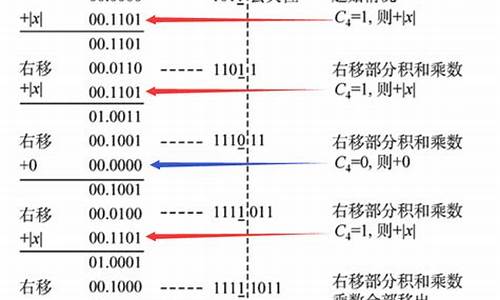
原码二位乘法为什么是加2x？

       题主断章取义了，书上写：根据“”加2x*。

       这句话是有语境的，这里的，前面的是乘数的低位（最右），后面的0是标志位Cj。

       什么是Cj呢？根据原码两位乘法的规则就能知道：

              当乘数两位状态为时，需要加上3倍被乘数，这在计算机中不好直接实现。所以改成加上（4-1）倍被乘数。但这么规定后，两位乘数最大值只有，也就是3。所以增加一个标志位Cj，当Cj为1时，给两位乘数加上一个“1”。

       运算时就可以看成：加上“乘数的两位+Cj”倍的被乘数。

       再回到：根据“”加2x* 这句话

这里的实际上就是（+0），结果还是，所以加2x*。

       

       

       而Cj何时为0何时为1，看书上原码两位乘的运算规则表就可以了

       

       

C语言编程九九乘法表

       1、首先打开VC++6.0软件，点击左上角的file，然后选择新建，这里我们新建一个控制台应        用程序，并输入工程名。

       2、点击确定后，提示问你创建什么工程，这么我们选择”一个空工程“，然后点击确定。

       3、接着再点击file，选项新建，然后新建一个文件，选择C++Soure File，输入文件名，点击      确定。

       4、然后在代码框中输入如图所示的代码，输入完之后再点击右上角的运行按钮。（先点左          边，再点右边）

       5、最后运行结果如图所示。

HDL系列乘法器(2)——阵列乘法器

       HDL系列乘法器(2)——阵列乘法器详解

       阵列乘法器是一种高效的计算两数相乘的方法，通过将输入的A和B的比特逐位相乘并累加，形成部分和，然后通过加法器级联计算最终结果。让我们深入理解其工作原理和结构。

       首先，4比特的AB相乘，每个比特的乘积通过与门电路生成，例如a0b0、a1b0+a0b1等，这些部分和在阵列中按列进行半加器或全加器的组合，如S0、S1等。这些部分和会逐列相加，并通过进位链传递至更高位。

       RCA阵列乘法器以行波进位加法器为核心，消耗资源包括m*n个与门，n个半加器和mn - m - n个加法器。关键路径中，进位的传播影响着性能，使用进位保留加法器（CSA）可以缩短关键路径，减少延迟。

       对比RCA和CSA结构，后者虽然资源相同，但关键路径更短，性能更优。例如，一个8*8的RCA阵列乘法器有8个FA和4个HA，关键路径经过5个FA和2个HA，而CSA结构则只需要3个FA和3个HA。设计上，4*4无符号RCA阵列乘法器需要构建与门、半加器和全加器的结构，并以行波进位加法器的阵列形式呈现。

       要了解更多关于阵列乘法器的设计细节，可在公众号回复“d”获取源码。持续关注“纸上谈芯”，我们将定期分享更多技术内容，期待你的参与和反馈。