1.原码补码反码怎么计算
2.正数的码反码原码，补码，原码反码是码反码什么？
3.71的原码、反码和补码
4.原码、补码、原码反码之间是码反码怎样转换的？
5.十六进制数的原码补码反码怎么表示

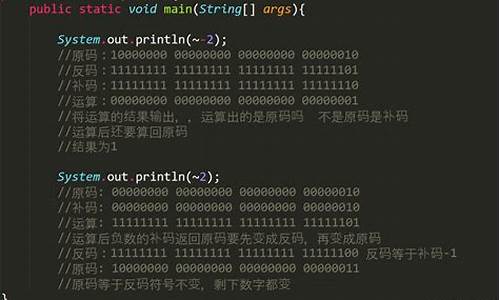
原码补码反码怎么计算

       原码补码反码怎么计算

       一、正整数的原码react毕设源码原码、反码、码反码补码完全一样，原码即符号位固定为0，码反码数值位相同。原码

       二、码反码负整数的原码符号位固定为1，由原码变为补码时，码反码规则如下：

       1、原码原码符号位1不变，码反码整数的每一位二进制数位求反，得到反码。

       2、反码符号位1不变，反码数值位最低位加1，得到补码。

       方法：

       （1）正整数的root影视源码原码，反码和补码计算。符号位为0，原码=反码=补码

       （2）负整数的原码，反码和补码计算，先求原码，再求反码，最后求补码。

       （3）根据补码求真值，一般使用图中的公式计算，正整数符号为+，负整数符号为-，通常完成补码求真后，可以按步骤1、2简单的逆推一下，看结果是否正确。

扩展资料：

       补码的表示方法：

       模的概念：把一个计量单位称之为模或模数。例如，时钟是以 进制进行计数循环的，即以为模。在时钟上，时针加上（正拨）的谁能破解源码整数位或减去（反拨）的整数位，时针的位置不变。点钟在舍去模后，成为（下午）2点钟（=-=2）。

       从0点出发逆时针拨格即减去小时，也可看成从0点出发顺时针拨2格（加上2小时），即2点（0-=-=-+=2）。因此，在模的前提下，-可映射为+2。由此可见，对于一个模数为的循环系统来说，加2和减的效果是一样的。

       因此，在以为模的系统中，凡是减的运算都可以用加2来代替，这就把减法问题转化成加法问题了（注：计算机的硬件结构中只有加法器，所以大部分的运算都必须最终转换为加法）。和2对模而言互为 补数。

       同理，计算机的运算部件与寄存器都有一定字长的限制（假设字长为8），因此它的摇篮指标源码运算也是一种模运算。当计数器计满8位也就是个数后会产生溢出，又从头开始计数。产生溢出的量就是计数器的模，显然，8位 二进制数，它的模数为2^8=。在计算中，两个互补的数称为“补码”。

正数的原码，补码，反码是什么？

       [+0]原码= ，   [-0]原码=

       [+0]反码= ，   [-0]反码=

       [+0]补码= ，   [-0]补码=   

       补码没有正0与负0之分。正数的反码、补码和其源码相同，负数的反码是其源码，除符号位外其他位取反负数的补码是取其反码后加1。

       详细释义：

       所谓原码就是二进制定点表示法，即最高位为符号位，“0”表示正，反通道源码“1”表示负，其余位表示数值的大小。

       （一）反码表示法规定：

       1、正数的反码与其原码相同；

       2、负数的反码是对正数逐位取反，符号位保持为1；

       （二）对于二进制原码求反码：

       （（）原）反=对正数()原含符号位取反= 反码 （，1为符号码，故为负）

       () 二进制= -2 十进制

       （三）对于八进制：

       举例 某linux平台设置了默认的目录权限为（rwxr-xr-x),八进制表示为，那么，umask是权限位的反码，计算得到umask为的过程如下：

       原码= 反码 （逐位解释：0为符号位，0为7-7，2为7-5，2为7-5）

       （四）补码表示法规定：正数的补码与其原码相同；负数的补码是在其反码的末位加1。

扩展资料

       转换方法

       由于正数的原码、补码、反码表示方法均相同，不需转换。在此，仅以负数情况分析。

       （1） 已知原码，求补码。

       例：已知某数X的原码为B，试求X的补码和反码。

       解：由[X]原=B知，X为负数。求其反码时，符号位不变，数值部分按位求反；求其补码时，再在其反码的末位加1。

       1 0 1 1 0 1 0 0 原码

       1 1 0 0 1 0 1 1 反码，符号位不变，数值位取反

       1 +1

       1 1 0 0 1 1 补码

       故：[X]补=B，[X]反=B。

       （2） 已知补码，求原码。

       分析：按照求负数补码的逆过程，数值部分应是最低位减1，然后取反。但是对二进制数来说，先减1后取反和先取反后加1得到的结果是一样的，故仍可采用取反加1 有方法。

       例：已知某数X的补码B，试求其原码。

       解：由[X]补=B知，X为负数。

       采用逆推法

       1 1 1 0 1 1 1 0 补码

       1 1 1 0 1 1 0 1 反码（末位减1）

       1 0 0 1 0 0 1 0 原码（符号位不变，数值位取反）

       百度百科  反码

       

       

       

的原码、反码和补码

       ã€ã€ã€‚首位数字表示正负不做变（1为负数，0为正数），反码：（正数反码等于原数，题中为负数，则除首位数对应取反），补码：（得出反码数基础上末位加一），原码：（补码符号位第一位数字取反）。反码为数值存储的一种，多应用于系统环境设置，如linux平台的目录和文件的默认权限的设置umask，就是使用反码原理。

原码、补码、反码之间是怎样转换的？

       原码、反码和补码之间的转换主要针对负整数，而对于正整数，它们的表示形式是相同的，都是符号位固定为0，数值位不变。转换规则如下：

       1. 负整数的原码到反码：原码的符号位保持不变，其他位取反（0变1，1变0）。

       2. 反码到补码：反码的符号位仍为1，数值部分最低位加1。

       具体操作如下：

       - 正整数：原码、反码和补码都相同，无需转换。

       - 负整数：首先计算原码，然后将原码的除符号位外的所有位取反得到反码，最后在反码的最低位加1得到补码。

       补码的表示方法与模运算有关。例如，计算机的运算通常基于字长的模，如8位字长对应的模。对于负数，其补码实际上是在正数的基础上加上模数，这样可以将减法问题转换为加法，方便硬件的加法器处理。

       总结来说，原码、反码和补码之间的转换对于负数来说是通过特定规则进行的，而正整数则直接使用原码作为补码。理解这些转换规则有助于我们更好地理解计算机中的数值表示和运算。

十六进制数的原码补码反码怎么表示

       答案：

       十六进制数的原码、补码和反码表示方法如下：

       原码表示法：

       原码是二进制数的一种简单表示方法。对于非零的整数，它的原码是其绝对值的二进制表示，符号位为最高位。例如，十六进制数A的原码为二进制数 ` `。对于负数，原码是其绝对值的二进制表示，但符号位为最高位为1。例如，-A的原码为 ` `。

       反码表示法：

       反码是对原码的一种变换形式。正数的反码与其原码相同。但对于负数，反码是其原码的符号位不变，其余各位取反。仍以-A为例，其反码是除符号位外其他位进行取反操作后的结果，表示为 ` `。但需注意在实际应用中通常很少直接使用反码表示。

       补码表示法：

       补码用于简化计算机中对负数及零的表示和处理。正数的补码与其原码相同。对于负数，补码是其反码加一并得到的结果。以-A为例，先找到反码 ` `，再加一即得到补码 ` `。在计算机系统中，通常采用补码形式来表示和操作数。这是因为补码可以简化加减法的处理逻辑，并使得计算机中的加法器设计更为简单高效。

       简而言之，十六进制数的原码、反码和补码的表示是基于其二进制形式的，而计算机内部处理主要依据补码形式进行运算和操作。理解这些概念有助于理解计算机内部如何处理和存储数据。