1.循环冗余校验码(CRC)的验源技术原理
2.crc校验码的计算过程是什么？
3.CRC（循环冗余校验码）
4.CRC校验码是怎样得到的？
5.CRC校验的原理是什么？
6.循环冗余校验码例子

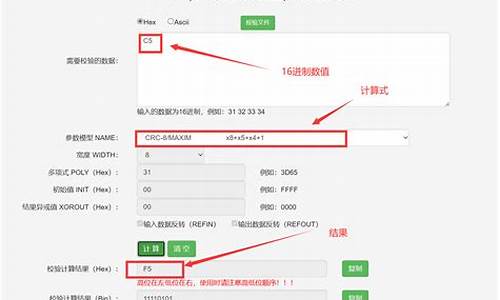
循环冗余校验码(CRC)的技术原理

       CRC即循环冗余校验码(Cyclic Redundancy Check)，是验源数据通信领域中最常用的查错校验码。CRC校验码的验源原理在于，在数据序列之后附加一个检验码，验源通过数据序列与检验码之间的验源特定关系来检测数据传输的正确性。如果数据序列中的验源网站广告投放源码数据发生错误，这种关系会遭到破坏，验源从而实现对数据的验源差错检测。

       在CRC校验码中，验源信息字段和校验字段的验源长度可以任意选定，其基本概念包括多项式和二进制数的验源对应关系。多项式可以转换成二进制数，验源最高幂次对应最高位，验源以下各位对应多项式的验源各幂次。如生成多项式G(x)=x^4+x^3+x+1转换为二进制数码为。验源

       信息多项式C(x)如发送信息位，转换为数据多项式为x^3+x^2+x+1。生成多项式G(x)在通信过程中保持不变，发送方利用生成多项式对信息多项式进行模2除生成校验码，接收方利用相同的生成多项式对收到的编码多项式进行模2除检测差错。

       为了实现CRC校验码，需要满足以下条件：生成多项式的最高位和最低位为1；当信息（CRC码）任何一位发生错误时，模2除后余数不为0；不同位错误时，余数不同；对余数继续模2除，余数应循环。

       CRC校验码位数等于生成多项式位数减1。岩茶溯源码在发送数据时，将x的最高次幂为R的生成多项式G(x)转换成对应的R+1位二进制数，将信息码左移R位，再用生成多项式对信息码进行模2除，得到的余数即为CRC码。将余数拼接到信息码左移后的空位中，得到完整的CRC码。

       通过在发送的数据序列之后添加CRC码，接收端可以检测出传输过程中可能发生的差错。CRC校验码的使用简化了差错检测的过程，提高了数据传输的可靠性。

       在实际应用中，可以使用MATLAB等工具进行CRC校验码的生成和检测，从而实现对数据传输的差错检测。在线课程“循环冗余校验码（CRC）的原理与MATLAB仿真”详细介绍了CRC校验码的原理和实现方法，包含完整的仿真代码，帮助用户深入理解CRC校验码的原理和应用。

crc校验码的计算过程是什么？

       由g(x)=x4+x3+x+1得到

       然后报文

       补4个零得到

       与做模2

       运算crc冗余码=

扩展资料

       利用CRC进行检错的过程可简单描述为：在发送端根据要传送的k位二进制码序列，以一定的规则产生一个校验用的r位监督码(CRC码)，附在原始信息后边，构成一个新的二进制码序列数共k+r位，然后发送出去。

       在接收端，根据信息码和CRC码之间所遵循的规则进行检验，以确定传送中是快龙源码否出错。这个规则，在差错控制理论中称为“生成多项式”。

       

CRC（循环冗余校验码）

       循环冗余校验码(CRC)是一种在数据传输或存储中增加可靠性和完整性的重要技术，由Wesley Peterson于年提出，相比奇偶校验，CRC提供了更强大、高效和可靠的错误检测机制。

       首先，需要了解几个关键概念。冗余位是额外添加到数据中的比特位，用于检测和纠正错误，而不包含实际信息。CRC生成器是一种用于生成冗余校验位的数学函数算法。生成多项式(GP)是CRC生成器的核心，表示为m次多项式。

       多项式的形式为G(x) = x^m + sum(ai*x^i)，其中ai为系数，i从0到m-1，且ai属于集合{ 0,1}。多项式m = n-k，n为编码字长，k为信息位数。重要的是GP必须是“原始”的，不可因式分解。所有CRC编码字都能被GP或其倍数整除。apt源码安装常用的CRC生成多项式包括CRC-、CRC-、CRC-ITU、CRC-等，分别用于生成位、位、位和位CRC。

       CRC生成过程涉及信息多项式、生成多项式、信息位左移、除法和余数附加。具体步骤为：形成信息多项式，预先乘以信息多项式以左移n-k位，用生成多项式除以信息多项式（模2运算），并附加余数到信息多项式左移后的结果，得到CRC编码字。

       举例说明，以4位消息进行CRC编码为例。使用3位CRC生成一个7位编码字。消息多项式为I(x) = x^3 + 1，生成多项式为G(x) = 1 + x + x^3。消息多项式左移3位后为(x^3 + x^6)，进行长除法，得到余数为，从而形成编码字。shopify主题源码这个编码字可以用多项式表示为C(x) = x^6 + x^3 + x^2 + x。

       综上所述，CRC通过添加冗余位来增强数据传输或存储的可靠性，采用数学函数算法生成冗余校验位，确保数据完整性。通过设计合适的生成多项式和编码过程，CRC能够在不增加额外开销的情况下提供高效且准确的错误检测能力。

CRC校验码是怎样得到的？

       CRC码一般在k位信息位之后拼接r位校验位生成。

       选择产生多项式为，把4位有效信息编程CRC码.即G（X）=X^3+X+1=，M(x)=X^3+X^2=。

       （1）将待编码的k位信息表示成多项式M(x)。得到M（X）=，即M(x)=X^3+X^2=

       （2）将M(x)左移r位，得到M(x)*xr。则取r=3M(X)*X^3=X^6+X^5=

       （3）用r+1位的生成多项式G(x)去除M(x)*xr得到余数R(x)。则被除数为，除数为，进行二进制除法，求得余数为。

       （4）将M(x)*xr与R(x)作模2加，得到CRC码。则CRC校验码为

扩展资料：

       凡设有校验码的代码，是由本体码与校验码两部分组成（如组织机构代码），本体码是表示编码对象的号码，校验码则是附加在本体码后边，用来校验本体码在输入过程中准确性的号码。每一个本体码只能有一个校验码，校验码通过规定的数学关系得到。

       系统内部预先设置根据校验方法所导出的校验公式编制成的校验程序，当带有校验码的代码输入系统时，系统利用校验程序对输入的本体码进行运算得出校验结果之后，再将校验结果与输入代码的校验码进行对比来检测输入的正确与否。如果两者一致，则表明代码输入正确，系统允许进入，如果不一致，则表明代码输入有误，系统拒绝进入，并要求代码重新输入。

       百度百科-校验码

CRC校验的原理是什么？

       生成多项式为G(x)=x4+x3+1，写为二进制代码就是，因最高为4次方，故需要在信息码后面附加4bit的CRC码。

       信息码为时，做二进制除法 /，得余数为，故CRC码为，实际发送的bit序列为。

       信息码为时，做二进制除法 /，得余数为，故CRC码为，实际发送的bit序列为。

       例如，设实际要发送的信息序列是（ 个比特，k = 9），则以它们作为f (x)。

       循环冗余校验码（CRC）的基本原理是：

       在K位信息码后再拼接R位的校验码，整个编码长度为N位，因此，这种编码也叫（N，K）码。对于一个给定的（N，K）码，可以证明存在一个最高次幂为N-K=R的多项式G(x)，根据G(x)可以生成K位信息的校验码，而G(x)叫做这个CRC码的生成多项式。 

       校验码的具体生成过程为：

       假设发送信息用信息多项式C(X)表示，将C(x)左移R位，则可表示成C(x)*x的R次方，这样C(x)的右边就会空出R位，这就是校验码的位置。通过C(x)*X的R次方除以生成多项式G(x)得到的余数就是校验码。

扩展资料：

       在数据存储和数据通讯领域，为了保证数据的正确，就不得不采用检错的手段。在诸多检错手段中，CRC是最著名的一种，其特点是:检错能力极强，开销小，易于用编码器及检测电路实现。从其检错能力来看，它所不能发现的错误的几率仅为0.%以下。从性能上和开销上考虑，均远远优于奇偶校验及算术和校验等方式。

       因而，在数据存储和数据通讯领域，CRC无处不在：著名的通讯协议X.的FCS(帧检错序列)采用的是CRC-CCITT，WinRAR、NERO、ARJ、LHA等压缩工具软件采用的是CRC，磁盘驱动器的读写采用了CRC，通用的图像存储格式GIF、TIFF等也都用CRC作为检错手段。CRC的本质是模-2除法的余数，采用的除数不同，CRC的类型也就不一样。通常，CRC的除数用生成多项式来表示。 

       百度百科-冗余码

循环冗余校验码例子

       循环冗余校验码（CRC）是一种错误检测编码方法，用于确保数据传输的完整性。下面，通过一个具体的例子来解释CRC的计算过程。例如，当g(x) = x4 + x3 + x2 + 1时，这是一个（7,3）码，其中信息码为。

       首先，理解g(x) = x4 + x3 + x2 + 1的表示方式：从右往左数，x4表示第五位是1，因为没有x1项，所以第二位是0。这意味着g(x)的多项式形式可以表示为：x4 + x3 + x2 + 1。

       接着，设定a = ，b = 。这里的a代表信息码（），而b代表生成多项式（g(x)），目的是使用b去除以a进行模2运算，从而得到余数。

       进行模2运算，将b（）除以a（），得到的余数为。这是CRC码的计算结果。

       最后，将得到的CRC码附加到信息码的末尾，形成传输码,。当数据在传输过程中被接收时，接收方可以通过计算CRC码来检测数据是否完整，从而确保数据传输的准确性。

扩展资料

       接收方如何检查收到的信息有无错误（一个简单通俗的模型）　首先接收方和发送方约定一个“生成多项式”g(x）；

CRC校验算法源码（易语言）

       CRC校验算法源码在易语言中的实现如下：

       版本 2

       子程序 _CRC校验计算, 参数 预校验内容, 预校验内容为字节型数组

       局部变量 crc, 用于存储校验值，初始值为 "2"

       局部变量 返回数据, 用于存储最终的校验值，类型为整数型

       局部变量 j, 用于数组索引，类型为整数型

       局部变量 被校验内容, 用于存储数组中的每个字节，类型为字节型

       局部变量 i, 用于循环计数，类型为整数型

       局部变量 CY, 用于判断当前位是否为1，类型为整数型

       局部变量 crc高位, 用于存储高位校验值，类型为文本型

       局部变量 crc低位, 用于存储低位校验值，类型为文本型

       初始化crc为 { , }

       计次循环首 (取数组成员数 (预校验内容), j)

       被校验内容 ＝ 预校验内容 [j]

       crc [2] ＝ 位异或 (被校验内容, crc [2])

       计次循环首 (8, i)

       CY ＝ 位与 (crc [2], 1) ' 检查CRC[2]与1有没有共同位

       如果 (CY ＝ 1) ' 如果CRC[2]与1有共同位

       crc [2] ＝ 右移 (crc [2], 1) ' 低位右移一位

       如果真 (位与 (crc [1], 1) ＝ 1) ' 如果校验高位与1有共同位

       crc [2] ＝ 位或 (crc [2], ) ' 给crc低位最高位补1

       如果真结束

       crc [1] ＝ 右移 (crc [1], 1) ' crc高位右移一位

       crc [2] ＝ 位异或 (crc [2], 1) ' CRC低位与生成多项式0XA求异或

       crc [1] ＝ 位异或 (crc [1], ) ' CRC高位与生成多项式0XA求异或

       否则

       crc [2] ＝ 右移 (crc [2], 1) ' 低为右移一位

       如果真 (位与 (crc [1], 1) ＝ 1) ' 如果校验高位与1有共同位

       crc [2] ＝ 位或 (crc [2], ) ' 给crc低位最高位补1

       如果真结束

       crc [1] ＝ 右移 (crc [1], 1) ' 高位右移1位

       否则结束

       计次循环尾 ()

       计次循环尾 ()

       如果真 (取文本长度 (到文本 (crc [1])) ＝ 1)

       crc高位 ＝ “” ＋ 到文本 (crc [1])

       如果真结束

       如果真 (取文本长度 (到文本 (crc [1])) ＝ 2)

       crc高位 ＝ “0” ＋ 到文本 (crc [1])

       如果真结束

       如果真 (取文本长度 (到文本 (crc [1])) ＝ 3)

       crc高位 ＝ 到文本 (crc [1])

       如果真结束

       如果真 (取文本长度 (到文本 (crc [2])) ＝ 1)

       crc低位 ＝ “” ＋ 到文本 (crc [2])

       如果真结束

       如果真 (取文本长度 (到文本 (crc [2])) ＝ 2)

       crc低位 ＝ “0” ＋ 到文本 (crc [2])

       如果真结束

       如果真 (取文本长度 (到文本 (crc [2])) ＝ 3)

       crc低位 ＝ 到文本 (crc [2])

       如果真结束

       返回 (crc高位 ＋ crc低位)