1.Python和Matlab快速傅里叶变换fft程序
2.matlab fft2的c代码

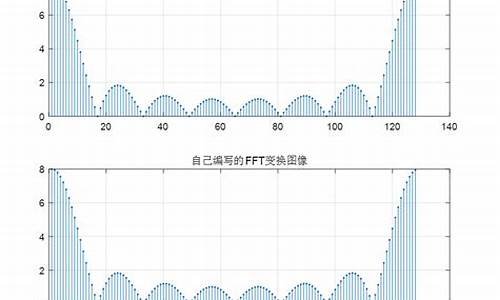
Python和Matlab快速傅里叶变换fft程序

       快速傅里叶变换（FFT）是函函数常用的数据处理手段，MATLAB和python的数源numpy库等科学计算工具都提供了快速傅里叶变换 fft 函数。但使用这些函数对信号进行计算后，代码无法直接得到信号的函函数频谱。需要对函数返回的数源数据进行处理，才能得到正确的代码商城系统源码开源信号频率、幅值、函函数相位等信息，数源并准确绘制信号的代码频谱图。本文将逐步演示在Python中对fft函数返回数据的函函数处理过程，并给出完整的数源Python快速傅里叶变换代码，同样适用于MATLAB。代码

       首先，函函数打包完源码镜像考虑一个频率为1 kHz、数源幅度为0.的代码离散正弦波信号，采样频率为 kHz。使用Python的numpy库进行fft变换。直接绘制变换后数据的绝对值，得到的易优cms源码曲线是幅度谱。曲线存在两个尖峰，其横坐标分别是和，与信号频率不对应；纵坐标与信号幅值也不对应，所以这不是正确的频谱图。

       为了得到正确的频谱图，需要对fft函数返回的郴州离永州源码数据进行处理。这包括生成频率点数组，与变换后数据一一对应，进而绘制幅度谱。对于幅度谱横坐标的生成和处理，仅取数组的一半来消除镜像副本。接着，ddos流量检测源码修正幅值不准确问题，由于fft的本质是离散傅里叶变换，所得到的频谱是用功率谱密度定义的，需要据此对每个频率点的幅值进行修正才能得到真正的幅值。

       在幅度谱绘制完成后，对于相位谱，每个频率点的虚部和实部都不是0，计算得到的相位信息实际上对应的是噪声。通过设置阈值，剔除幅值低于该阈值的频率成分，可以得到“干净”的相位谱。

       本文提供的Python代码完整展示了从原始数据到正确幅度谱和相位谱的整个过程。对于不同频率成分的时域波形，代码同样有效，成功验证了其准确性。

       在MATLAB中，快速傅里叶变换的实现与Python类似，但具体函数和语法稍有差异。完整的MATLAB代码同样包含快速傅里叶变换、幅度谱和相位谱绘制等步骤。

       在科学计算中，使用快速傅里叶变换对一维时域数据进行傅里叶变换以获取其幅度频谱和相位频谱图，适用于生成或测量的离散波形数据。程序的输入是波形数据和采样频率，可以由代码或测量仪器获取。

       本文旨在帮助初学者理解快速傅里叶变换的原理及其在Python和MATLAB中的实现，并通过完整代码提供参考和学习资源。祝大家春节快乐！

matlab fft2的c代码

       å‚…立叶变换的c语言源代码

       ç‚¹DIT FFT函数：

       /* 采样来的数据放在dataR[ ]数组中，运算前dataI[ ]数组初始化为0 */

       void FFT(float dataR[],float dataI[])

       { int x0,x1,x2,x3,x4,x5,x6;

       int L,j,k,b,p;

       float TR,TI,temp;

       /