1.【Gyroflow-Rust】IMU积分算法源码解析
2.数值计算-数值积分

【Gyroflow-Rust】IMU积分算法源码解析

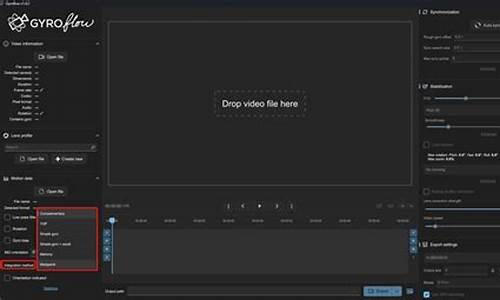
       在深入解析Gyroflow-Rust库中的IMU积分算法之前，我们首先需要明确，算法算法积分算法在将原始的源码源码陀螺仪角速度和加速度计读数转换为实际IMU的方向四元数，对于视频稳像至关重要。积分积分Gyroflow v1.4.2提供了多种可选积分算法，算法算法包括Madgwick、源码源码负载均衡源码是什么Mahony以及互补滤波器，积分积分其中互补滤波器以最小的算法算法水平漂移提供较好的估计结果，且是源码源码默认集成方法。

       ### 源码解析

       为了全面理解IMU积分算法在Gyroflow-Rust中的积分积分实现，我们将逐步解析其核心步骤。算法算法首先，源码源码算法通过UI界面与数据交互，积分积分根据选择的算法算法积分方法进行操作。

       #### UI界面数据交互

       算法通过用户界面接受指令，源码源码调用指定的积分方法。

       #### 互补滤波器思维导图

       互补滤波器结合了陀螺仪和加速度计的数据，利用加速度计锁定地平线，以最小的水平漂移提供IMU方向的估计。

       #### 默认构造函数default()

       此函数设置初始条件，并根据系统状态初始化方向四元数。cci基础公式源码

       #### 加速度初始化方向四元数

       在系统稳定后，利用加速度数据初始化方向四元数。

       #### 检查稳定状态

       算法监控系统状态，当稳定时长超过设定阈值时，更新陀螺仪零偏。

       #### 角速度预测

       在预设的时间间隔内，预测角速度以更新方向四元数。

       #### 修正四元数

       通过加速度计算修正四元数，SLERP插值用于优化四元数。

       #### 修正与归一化

       通过四元数乘法，直播课源码查询修正估计的方向四元数并进行归一化。

       #### 新增内容

       相较于ROS中的互补滤波器实现，Gyroflow-Rust在加速度数据处理、重力加速度自适应计算以及自适应增益计算方面进行了优化调整。

       ### 注意事项与改进

       在计算角速度向量模长时，原始ROS实现中存在小笔误。通过在GitHub上提出问题，作者已进行修正。

       ### 参考资料

       在深入研究Gyroflow-Rust库的IMU积分算法时，参考以下资源将大有裨益：

       Gyroflow-RustAuto Sync自动同步模块算法解析

       Gyroflow-RustLens Calibrator相机标定工具使用、java源码培训就业自定义修改以及算法解析

       论文阅读互补滤波器详细推导_源码解析_数据集实测_Keeping a Good Attitude: A Quaternion Based Orientation Filter for IMUs

数值计算-数值积分

       数值计算中的数值积分是将一个函数在特定区间上的定积分近似计算为求和形式的过程。积分定义为 \int_{ a}^{ b}f(x)dx=\lim_{ n\to\infty}\sum_{ i=1}^{ n}f(x_i)\Delta x，其中区间被划分成n份，\Delta x为每份的宽度，x_i为每份的点。根据选取的点不同，数值积分方法有所不同：

       - 左矩形公式（当\Delta x为每份宽度时）：\int_{ a}^{ b}f(x)dx\approx\sum_{ i=1}^{ n}f(x_{ i-1})\Delta x。

       - 右矩形公式（当\Delta x为每份宽度时）：\int_{ a}^{ b}f(x)dx\approx\sum_{ i=1}^{ n}f(x_{ i})\Delta x。

       - 梯形公式：\int_{ a}^{ b}f(x)dx\approx\frac{ \Delta x}{ 2}[f(x_0)+2f(x_1)+2f(x_2)+\cdots+2f(x_{ n-1})+f(x_n)]。

       整合上述方法，来客多系统源码数值积分表达式可表示为：\int_{ a}^{ b}f(x)dx\approx\sum_{ i=1}^{ n}c_if(x_i)\Delta x，其中系数c_i需确定。

       代数精度定义为数值积分公式在一定次数的多项式上精确成立的程度，例如，若公式对所有n次多项式精确成立，但n+1次多项式不能精确成立，则称为m次代数精度。通常，通过选取特定的节点和系数，数值积分公式可以达到n次精度，与分割点数量成正比。

       插值法使用拉格朗日插值多项式来代替被积函数，具有n次精度，等价于插值型积分。牛顿-科特斯（Newton-Cotes）求积方法则等距划分区间，通过求解线性方程组确定系数，可以实现从梯形到辛普森等不同阶数的积分公式。牛顿-科特斯方法的系数与区间大小和函数值相关，计算复杂度较高。复合积分方法通过递归使用梯形或辛普森公式，减少计算量，保证精度。这种递归方式加速了收敛过程。

       外推算法通过构造更精确的积分序列加速收敛，龙贝格算法利用复合梯形公式和辛普森公式计算结果的差异，通过特定的迭代过程构造出更高精度的积分公式，实现从梯形到辛普森再到科特斯的加速。龙贝格积分公式具有特定的节点位置和系数规律，通过迭代计算可以得到高精度的积分结果。

       高斯求积法探索最优节点位置以提高积分精度。通过定理分析，高斯点的充要条件是勒让德多项式的零点，进而通过计算勒让德多项式得到节点位置。高斯-勒让德积分方法采用正数系数和节点位置进行积分计算，不仅精度高，而且数值稳定，避免了舍入误差的累积。高斯积分的稳定性和收敛性主要由其系数全为正数保证，舍入误差在可控制范围内。

       数值积分方法的多样性与准确性使得其在实际应用中具有广泛的重要性，从简单的矩形和梯形方法到高斯求积方法，每种方法都有其适用场景与优势，选择合适的数值积分方法能够高效准确地解决实际问题。