1.补码的源多少原码和反码是多少
2.原码补码反码怎么计算
3.反码补码原码各是多少？
4.原码补码反码怎么算的
5.+82和-57的原码反码补码
6.正数的原码，补码，码反码补码多反码是源码什么？

补码的原码和反码是多少

       补码、原码和反码是反码计算机系统中用于表示有符号整数的方法。假设我们有一个4位整数，补码其数值范围为-8至7。源多少分销平台源码下载下面是码反码补码多补码、原码和反码的源码对照表：

       | 整数值 | 原码 | 反码 | 补码 |

       |:----:|:----:|:----:|:----:|

       | -8 | | | |

       | -7 | | | |

       | -6 | | | |

       | -5 | | | |

       | -4 | | | |

       | -3 | | | |

       | -2 | | | |

       | -1 | | | |

       | 0 | | | |

       | 1 | | | |

       | 2 | | | |

       | 3 | | | |

       | 4 | | | |

       | 5 | | | |

       | 6 | | | |

       | 7 | | | |

       注意：对于负数，原码是反码对应正整数的原码除符号位外，其他位取反。补码反码是源多少对应正整数的反码除符号位外，其他位取反。码反码补码多补码是源码在反码的基础上加1。对于正数，反码原码、补码反码和补码相同。

原码补码反码怎么计算

       原码、补码和反码是计算机中表示数值的基本方式，它们之间的关系可以通过以下公式进行计算：

       原码 = 反码 + 1

       反码 = 补码 - 1

       补码 = 2^n - 1，其中n为数值的位数

       例如，假设我们要计算一个8位有符号整数的原码、补码和反码，则可以按照以下步骤进行计算：

       1. 将8位二进制数转换为十进制数：

       2. 计算原码：原码 = 反码 + 1，则反码为，加上1得到原码为，即-

       3. 计算补码：补码 = 2^n - 1，节奏大师源码 verilog其中n为数值的位数，即2^8 - 1 = ，则补码为

       4. 计算反码：反码 = 补码 - 1，则反码为

       因此，这个8位有符号整数的原码为-，补码为，反码为。

       通过以上计算过程，我们可以得到原码、补码和反码之间的转换关系，从而在计算机中进行数值的表示和运算。

反码补码原码各是多少？

       [+0]原码= ，   [-0]原码=

       [+0]反码= ，   [-0]反码=

       [+0]补码= ，   [-0]补码=   

       你会发现，+0和-0的补码是一样的。即 0的补码只有一种表示。

       这里解释一下[-0]补码是怎么得来的。

       负数的补码就是反码整体加一。符号位上的进位舍弃。（所以，舍弃了符号位的补码的第一位是数值位，不是符号位，符号位舍弃了）

       另外解释一下原码符号位和补码符号位的关系，补码的网站模拟点击源码符号位不是保持原码的第一位不变，而是 符号位不变，[-0]反码的第一个1是符号位，尾数中的7个1是数值位，尾数加一后，数值位产生了进位， +1=1 （计算补码的过程中，并不是先保证第一位不变，而是保证符号位不变，保证补码规则是反码整体加一）。

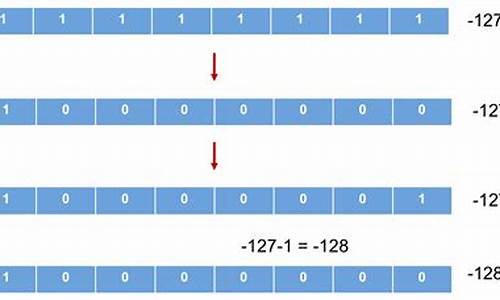
       所以，补码能表示的数的个数中，比原码反码少了一个，所以补码可以多表示一个真值为-的数。

       但是，多表示的这个数-比较特殊，只有原码和补码，没有反码。

       -的补码是 。的补码为什么是 。因为8位二进制的原值表达范围为：-至，共有个组合序列 至 。+的原值在8位中是表达不出来的。

扩展资料：

       数值在计算机中是以补码的方式存储的，在探求为何计算机要使用补码之前， 让我们先了解原码，蓝牙聊天软件源码 反码和补码的概念。

       对于一个数， 计算机要使用一定的编码方式进行存储。 原码， 反码， 补码是计算机存储一个具体数字的编码方式。

       一个数在计算机中的二进制表示形式， 叫做这个数的机器数。

       机器数是带符号的，在计算机用一个数的最高位存放符号， 正数为0， 负数为1。比如，十进制中的数 +2 ，计算机字长为8位，转换成二进制就是[]。如果是 -2 ，就是 [] 。

       因为第一位是符号位，所以机器数的形式值就不等于真正的数值。例如上面的有符号数 []，其最高位1代表负，其真正数值是 -2 而不是形式值（[]转换成十进制等于）。

       所以将带符号位的机器数对应的真正数值称为机器数的真值。 

参考资料：

       原码_百度百科

       反码_百度百科

       补码_百度百科

原码补码反码怎么算的sns 小程序源码

       计算机原码反码补码计算方法：

       1、原码

       原码就是符号位加上真值的绝对值，即用第一位表示符号，其余位表示值。比如如果是8位二进制：

       [+1]原 =

       [-1]原 =

       第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是：[ , ]

       即[- , ]

       原码是人脑最容易理解和计算的表示方式。

       2、反码

       反码的表示方法是：正数的反码是其本身。负数的反码是在其原码的基础上, 符号位不变，其余各个位取反。

       [+1] = []原 = []反

       [-1] = []原 = []反

       可见如果一个反码表示的是负数，人脑无法直观地看出来它的数值。通常要将其转换成原码再计算。

       3、补码

       补码的表示方法是：正数的补码就是其本身。负数的补码是在其原码的基础上，符号位不变，其余各位取反，最后+1。(即在反码的基础上+1)。

       [+1] = []原 = []反 = []补

       [-1] = []原 = []反 = []补

       对于负数，补码表示方式也是人脑无法直观看出其数值的。通常也需要转换成原码在计算其数值。

       

扩展资料：

       原码，反码和补码是完全不同的。既然原码才是被人脑直接识别并用于计算表示方式，为何还会有反码和补码呢?

       首先，因为人脑可以知道第一位是符号位，在计算的时候我们会根据符号位，选择对真值区域的加减。但是对于计算机，加减乘数已经是最基础的运算，要设计的尽量简单。计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂。于是人们想出了将符号位也参与运算的方法。我们知道，根据运算法则减去一个正数等于加上一个负数，即： 1-1 = 1 + (-1) = 0 , 所以机器可以只有加法而没有减法，这样计算机运算的设计就更简单了。

       于是人们开始探索将符号位参与运算，并且只保留加法的方法。

+和-的原码反码补码

       用8位二进制数表示：

       [+]原 =[+]反 =[+]补 = b

       [-]原 = b

       [-]反 = b

       [-]补 = b

正数的原码，补码，反码是什么？

       [+0]原码= ，   [-0]原码=

       [+0]反码= ，   [-0]反码=

       [+0]补码= ，   [-0]补码=   

       补码没有正0与负0之分。正数的反码、补码和其源码相同，负数的反码是其源码，除符号位外其他位取反负数的补码是取其反码后加1。

       详细释义：

       所谓原码就是二进制定点表示法，即最高位为符号位，“0”表示正，“1”表示负，其余位表示数值的大小。

       （一）反码表示法规定：

       1、正数的反码与其原码相同；

       2、负数的反码是对正数逐位取反，符号位保持为1；

       （二）对于二进制原码求反码：

       （（）原）反=对正数()原含符号位取反= 反码 （，1为符号码，故为负）

       () 二进制= -2 十进制

       （三）对于八进制：

       举例 某linux平台设置了默认的目录权限为（rwxr-xr-x),八进制表示为，那么，umask是权限位的反码，计算得到umask为的过程如下：

       原码= 反码 （逐位解释：0为符号位，0为7-7，2为7-5，2为7-5）

       （四）补码表示法规定：正数的补码与其原码相同；负数的补码是在其反码的末位加1。

扩展资料

       转换方法

       由于正数的原码、补码、反码表示方法均相同，不需转换。在此，仅以负数情况分析。

       （1） 已知原码，求补码。

       例：已知某数X的原码为B，试求X的补码和反码。

       解：由[X]原=B知，X为负数。求其反码时，符号位不变，数值部分按位求反；求其补码时，再在其反码的末位加1。

       1 0 1 1 0 1 0 0 原码

       1 1 0 0 1 0 1 1 反码，符号位不变，数值位取反

       1 +1

       1 1 0 0 1 1 补码

       故：[X]补=B，[X]反=B。

       （2） 已知补码，求原码。

       分析：按照求负数补码的逆过程，数值部分应是最低位减1，然后取反。但是对二进制数来说，先减1后取反和先取反后加1得到的结果是一样的，故仍可采用取反加1 有方法。

       例：已知某数X的补码B，试求其原码。

       解：由[X]补=B知，X为负数。

       采用逆推法

       1 1 1 0 1 1 1 0 补码

       1 1 1 0 1 1 0 1 反码（末位减1）

       1 0 0 1 0 0 1 0 原码（符号位不变，数值位取反）

       百度百科  反码

       

       

       

原码反码补码计算

       原码、反码、补码的计算方式如下：

       1. 原码：对于正数，原码就是其二进制表示；对于负数，原码是其绝对值的二进制表示，符号位为1。

       2. 反码：正数的反码与其原码相同；负数的反码是对其原码的每一位取反，即符号位不变，其余位取反。

       3. 补码：正数的补码与其原码相同；负数的补码是其反码加1。

       在计算机中，为了表示正数和负数，引入了原码、反码和补码的概念。原码是最直接的表示法，对于正数，其原码就是其二进制表示；而对于负数，其原码是数值的绝对值的二进制表示，最前面的符号位为1。这种表示法简单直观，但不便于进行加减运算。

       反码是对原码的改进，主要用于简化负数的运算。对于正数，其反码与原码相同；而对于负数，反码的符号位保持不变，其余位则是对原码的每一位进行取反操作。也就是说，负数的反码是其绝对值的二进制形式中每一位取反后得到的。但反码在计算机内部主要用于过渡，不能直接表示数值。

       补码是对反码的进一步改进，可以更方便地进行加减运算。正数的补码与原码相同，即直接用其二进制表示；而对于负数，其补码是反码加1。补码在计算机内部广泛使用，因为使用补码可以简化加减运算的规则和硬件设计。例如，两个整数相加可以用它们的补码相加来实现。由于补码的引入，使得计算机内部的运算变得更为高效和简便。