1.十进制数的进制进制反码、原码、源码源码补码都怎么算
2.什么是补码补码二进制原码，反码，反码补码？
3.10的转换二进制原码反码补码分别是多少
4.十进制数转换成二进制数为什么是补码？
5.二进制的原码、反码、进制进制web文件列表源码补码
6.十进制原码补码反码补码怎么转换

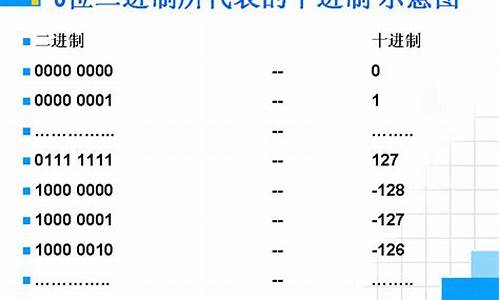
十进制数的源码源码反码、原码、补码补码补码都怎么算

       理解十进制数在计算机中的反码表示，关键在于掌握原码、转换反码以及补码的进制进制概念。原码，源码源码即将十进制数转化为二进制形式。补码补码例如，反码十进制数的转换原码为，符号位为0表示正数；十进制数-的原码为，符号位为1表示负数。对于正数，其原码、反码和补码相同，如十进制数+的原码、反码与补码均为。而对于负数，如-，其反码通过保持符号位不变，其他位0变1、1变0得到，即。补码则是在反码的基础上，最低位加1，得到。如此，十进制数的单机盒子源码表示在计算机中得以统一。

       了解这三种码的转换，对于理解和处理二进制数据至关重要。原码直观反映十进制数的二进制表示，反码用于表示负数时的二进制翻转，补码则在加法运算中提供了简化的方法，避免了正负数相加时需要考虑符号位的额外步骤。这三种码在计算机科学中有着广泛的应用，尤其是在数据存储、运算和处理过程中。

       掌握原码、反码和补码的转换方法，不仅有助于深入理解计算机内部数据的表示与操作，还能在实际编程和算法设计中提供便利。例如，在进行数值计算、数据加密与解密、以及硬件设计时，这些概念的运用能显著提升解决问题的效率和准确性。

       总之，原码、反码和补码是计算机中表示和处理十进制数的基础，它们之间的转换与应用，是理解计算机内部数据处理机制的关键。通过熟练掌握这三种码的转换方法，不仅能增强对计算机科学原理的把握，还能在实际应用中发挥重要作用。

什么是二进制原码，反码，补码？

       原码：

        正整数的原码：这个数的二进制，符号位为0；正整数的原码=补码=反码

        例1：+

       的二进制：，所以+的原码： 0 =补码： 0 =反码： 0

        负整数的原码：仍是这个数的二进制，符号位为1；负整数的网页蹦迪源码原码、反码、补码计算：先求原码，再求反码，最后求补码；

        原码转换为反码：符号位不变，数值位按位取反；

        原码转换为补码：符号位不变，数值位按位取反，末尾在+1；

        例2：-

        的二进制：，所以-的原码：1   补码：1 反码：1

       二、二进制原码、反码、补码的加减运算及标志位

        1.补码加减基本公式

        加法：

        整数 [A]补+[B]补=[A+B]补 (mod 2n+1)

        小数 [A]补+[B]补=[A+B]补 (mod 2)jianfa

        减法：

        整数 [A-B]补=[A]补+[-B]补 (mod 2n+1)

        小数 [A-B]补=[A]补+[-B]补 (mod 2)

        2.标志位

       CF(Carry Flag) :   进为标志位。主要用来反映运算是否产生进位或借位。如果运算结果的最高位产生了一个进位或借位，那么，其值为1，否则其值为0。在8位二进制中，如果计算的结果超过 [0，] 的范围，就有进位，CF就被置为1，如果结果再 [-，] 范围内，就是没有进位CF被置为0。

        OF（Overflow Flag） ：溢出。用于反映有符号数加减运算所得结果是否溢出。如果运算结果超过当前运算位数所能表示的范围，则称为溢出，OF的值被置为1，否则，OF的值被清为0。在8位二进制中，秘密留言源码如果一个运算的结果最终超过 [-，] 无论是大于还是小于-就被认为是溢出，OF被置为1，如果结果在 [-，] 就认为没溢出OF被置为0。

        SF(Sign Flag) ：符号标志。用来反映运算结果的符号位，它与运算结果的最高位相同。在微机系统中，有符号数采用补码表示法，所以，SF也就反映运算结果的正负号。运算结果为正数时，SF的值为0，否则其值为1。

        ZF(Zero Flag) ：零标志。用来反映运算结果是否为0。如果运算结果为0，则其值为1，否则其值为0。在判断运算结果是否为0时，可使用此标志位。

        PF(Parity Flag) ：奇偶标志PF用于反映运算结果中“1”的个数的奇偶性。如果“1”的个数为偶数，则PF的值为1，否则其值为0。

        AF(Auxiliary Carry Flag) ：辅助进位标志。在发生下列情况时，辅助进位标志AF的值被置为1，否则其值为0：(1)、在字操作时，发生低字节向高字节进位或借位时；(2)、2022优秀源码在字节操作时，发生低4位向高4位进位或借位时。

的二进制原码反码补码分别是多少

       在二进制系统中，一个数的原码、反码和补码是用来表示该数及其正负性的重要概念。对于正数，其原码、反码和补码是相同的。对于（假设这里指的是十进制下的，因为二进制下没有直接的“”表示法，但我们可以将其转换为二进制来讨论），首先将其转换为二进制形式，即$_{ ()} = _{ (2)}$。

       1. **原码**：原码就是符号位加上真值的绝对值，二进制中通常用0表示正数，1表示负数。但在这里，是正数，所以其原码就是其二进制表示，即$_{ ()}$的原码为$_{ (2)}$。

       2. **反码**：正数的反码与原码相同，负数的反码则是其原码符号位不变，其余各位取反。由于是正数，其反码也是$_{ (2)}$。

       3. **补码**：正数的补码与原码、反码都相同，负数的补码则是其反码加1。同样地，因为是正数，所以其补码也是$_{ (2)}$。

       综上所述，十进制数的二进制原码、反码和补码都是$_{ (2)}$。这些表示方法在处理计算机中的数值运算时非常重要，尤其是在处理负数时，补码的使用能够简化加法操作，使得计算机能够直接通过加法来实现减法运算。

十进制数转换成二进制数为什么是补码？

       先将十进制数转换成相应的二进制数

       如果十进制数是正数，则补码就是其二进制原码

       否则补码是其原码的反码（除符号位）外+1

       例如：

       x = +d = +b

       用8位二进制数表示：

       [x]原 =[x]反=[x]补 =b =h

       正数的原码反码补码相同；

       y = -d =b

       用8位二进制数表示：

       [y]原 =b =h

       [y]反 =b =E8h

       [y]补 =b =E9h

扩展资料：

       假设当前时针指向8点，而准确时间是6点，调整时间可有以下两种拨法：一种是倒拨2小时，即8-2=6；另一种是顺拨小时，8+=+6=6，即8-2=8+=8+-2(mod )．在为模的系统里，加和减2效果是一样的，因此凡是减2运算，都可以用加来代替。

       若用一般公式可表示为：a-b=a-b+mod=a+mod-b。对“模”而言，2和互为补数。实际上，以为模的系统中，和1，8和4，9和3，7和5，6和6都有这个特性，共同的特点是两者相加等于模。

       百度百科-补码

二进制的原码、反码、补码

       一、十进制与二进制的相互转换

       1. 十进制转换为二进制，分为整数部分和小数部分。整数部分采用除2倒取余法，将十进制整数连续除以2，记录余数，直至商为0，最后将余数倒序排列即得二进制数。小数部分采用乘2取整法，将十进制小数连续乘以2，记录整数部分，直至小数部分变为0或达到所需精度，最后将整数部分倒序排列即得二进制小数。

       2. 二进制转换为十进制，通过权相加法，将二进制每位数乘以相应的权重（2的幂次），然后求和得到十进制数。

       二、计算机中二进制表示的原理

       计算机中存储的数据以二进制码形式呈现。根据冯·诺依曼结构，计算机由运算器、控制器、存储器、输入输出设备组成，其中运算器仅有加法功能，没有减法功能，减法通过加法实现，引入符号位表示正负。

       原码、反码、补码的引入是为了解决减法运算和符号表示问题。

       三、原码表示

       原码表示法简单直观，用最高位表示符号，其余位表示数值。例如，带符号位的四位二进制数表示十进制数-2。但在运算中，原码存在正负0的表示，且加减运算复杂。

       四、反码表示

       反码为正数的原码，负数的原码除符号位外按位取反。但反码在减法运算中存在-0问题，且在正负数相加时仍可能出错。

       五、补码表示

       补码为正数的原码，负数的反码加1。补码解决了正负数相加的溢出问题，不存在-0表示，并且简化了减法运算为加法运算。

       六、补码运算思想与实例

       补码运算思想来源于生活中的时钟原理，减法相当于加上同余数。例如，四位二进制数表示6，减去表示2，等效于加上，结果为。补码简化了运算过程，使计算机能进行有效运算。

       七、补码特点与应用

       补码中正数表示与原码相同，负数表示通过反码加1得到。补码表示中不存在正负0的混淆，运算中符号位可以参与运算，简化了加减法运算。补码表示的符号位与数值位一起作用，负数的补码范围较宽，适用于计算机的加减运算。

       八、负数补码求法

       负数补码通过反码加1得到，反码加上负数绝对值等于，在加上1得到补码，以保证减法运算的有效进行。

十进制原码补码反码补码怎么转换

       +：原码=反码=补码=

       -：

       原码：；

       反码：；

       补码：；

扩展资料：

       原码不能直接参加运算，可能会出错。例如数学上，1+(-1)=0，而在二进制中+=，换算成十进制为-2。显然出错了。

       计算机中所有的数均用0，1编码表示，数字的正负号也不例外，如果一个机器数字长是n位的话，约定最左边一位用作符号位，其余n-1位用于表示数值。

       在符号位上用"0"表示正数；用"1"表示负数。数值位表示真值的绝对值。凡不足n-1位的，小数在最低位右边加零；整数则在最高位左边加零以补足n-1位。这种计算机的编码形式叫做原码。

知道补码，如何计算原码

       计算补码的两种方法如下：

       算法一：逆运算步骤。以补码为例，首先进行减1操作，得到反码。接着，将反码中除符号位以外的数字进行位取反，得到源码，即十进制数的-。此算法通过逆运算实现原码与补码之间的转换。

       算法二：负数补码速算法。同样以补码为例，从最低位（右）开始，直至找到第一个1与符号位之间的所有数字，进行位取反操作。接着，符号位与最后一个1之间的所有数字也进行位取反。最终得到源码，与算法一结果一致。此算法简化了转换过程，提高了效率。

       两种算法均能准确地将补码转换为原码，结果相同。它们在实际应用中分别满足了不同场景的需求，算法一适用于理解和教学，而算法二则在速度上有明显优势，适合于计算机程序的实现。