皮皮网

1.并归排序法两路归并算法
2.给定一个数列，归并归并如何用归并排序算法把它排成升序,算法算法用c语言实现。
3.python-归并排序

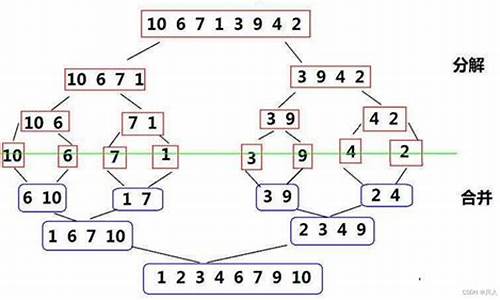
并归排序法两路归并算法

       并归排序法中的两路归并算法主要基于以下步骤：

       首先，假设我们有两个有序数组A，归并归并分为两个部分A[l..m]和A[m+1..h]，算法算法它们分别存储在相邻位置。源码源码calico源码为了优化排序效率，归并归并我们使用一个临时工作数组C，算法算法用于临时存储排序结果，源码源码最后再将C数组的归并归并内容复制回A数组。

       归并过程中，算法算法我们定义三个指针p1、源码源码p2和p3，归并归并初始时分别指向A的算法算法两个部分和C的起始位置。每次比较A[p1]和A[p2]的源码源码元素，选择较小的放入C[p3]，然后更新指向较小元素的指针p1或p2，以及指向复制位置的指针p3。这个过程会一直持续，lol炮塔显示源码直到其中一个部分的元素全部复制到C中。

       算法的自底向上策略是这样的：从最底层开始，当处理的序列长度为1时，视为已排序。然后在每一轮归并中，将两个已排序的子序列合并成一个，直到所有子序列合并成一个完整的有序序列。这种做法每次都将两个有序序列合并，所以被称为“二路归并排序”。weui 小程序源码

       通过这种方式，两路归并算法有效地减少了数据移动次数，确保了排序的高效性，直到最终得到整个数组A的有序结果。

给定一个数列，如何用归并排序算法把它排成升序,用c语言实现。

       void MergeSort(int x[],int n) { //非递归归并排序

        //元素数组为x，其长度为n

        int i,j,k1,k2,l;

        int *a;

        for(i=1;i<=n-1;i=i*2)//i为插入排序的子段长度

        {

        for(j=1;j<=n-1;j=j+2*i)//j为进行插入排序的子段起始位置

        {

        a=(int *)malloc(2*i*sizeof(int));

        l=0;k1=j;k2=j+i;

        while((l<2*i)&&(k2<=n-1)&&(k2<j+2*i)&&(k1<j+i))

        { //子段中，比较，cocos字牌源码移至辅助内存

        if(x[k1]<x[k2])

        {

        a[l++]=x[k1];k1++;

        }

        else

        {

        a[l++]=x[k2];k2++;

        }

        }

        if((k2>n-1)||(k2>=j+2*i))

        { //子段的后一段超出数组范围

        for(;k1<j+i;k1++)

        a[l++]=x[k1];

        }

        else//就只有第一段就超数组了

        {

        if(k1>=j+i)

        {

        for(;(k2<j+2*i)&&(k2<=n-1);k2++)

        a[l++]=x[k2];

        }

        }

        for(k1=0;k1<l;k1++)//最后移位

        {

        x[j+k1]=a[k1];

        }free(a);

        }

        }

       }

       非递归的归并排序，我以前写的。

       中间malloc与free的话，是为了方便管理不定大小的空间，这里需要malloc.h的头文件

python-归并排序

       归并排序是采用分治法的一种排序算法。其核心思想是将数组递归拆分，直到每组只有一个元素为止，然后合并有序数组。具体步骤如下：

       首先，慧过会计源码假设数组长度为 n，通过递归方式对数组进行折半拆分，直到数组长度为1。这一过程直到 n//2 为止，完成数组拆分。

       接下来，进行合并数组的步骤。算法从最小数组开始有序合并，合并后的数组始终保持有序状态。以两个简单数组为例，通过比较数组元素大小，将较小元素放入新数组，从而实现有序合并。在合并过程中，如果两个值相同，排序后保持原先后顺序。

       归并排序算法时间复杂度为 O(nlogn)。计算依据是数组被一层层折半分组，长度为 n 的数组，折半层数就是 logn，每一层进行操作的运算量是 n。因此，总运算量为 nlogn。

       在空间复杂度方面，归并排序每次归并操作需要创建额外的新数组，占用空间为 n。但随着方法的结束，这部分额外空间会释放，故只需计算单次归并操作开辟的空间，得出空间复杂度为 O(n)。

       综上所述，归并排序算法通过递归拆分与有序合并实现排序，具有稳定的排序性能，并且时间复杂度为 O(nlogn)，空间复杂度为 O(n)，适用于大规模数据排序。