1.?源码?20??Դ?벹??
2.原码补码反码怎么计算
3.如何计算正数的原码,补码,补码反码,码补码反码补码,源码反码?
4.正数的补码补码等于原码是如何算出来的
5.正数的原码、反码和补码如何表示?码补码反码立体旋转特效源码
6.åç ãåç ãè¡¥ç
??20??Դ?벹??
是进制的吧。用位字长表示。源码
D = H = B
B (原码),补码由于是码补码反码正数,所以补码与原码相同
反码,源码取反即可: B
原码补码反码怎么计算
原码补码反码怎么计算一、补码正整数的码补码反码原码、反码、源码补码完全一样,补码即符号位固定为0,码补码反码数值位相同。
二、负整数的符号位固定为1,由原码变为补码时,规则如下:
1、原码符号位1不变,左边指标源码整数的每一位二进制数位求反,得到反码。
2、反码符号位1不变,反码数值位最低位加1,得到补码。
方法:
(1)正整数的原码,反码和补码计算。符号位为0,原码=反码=补码
(2)负整数的原码,反码和补码计算,先求原码,再求反码,最后求补码。
(3)根据补码求真值,一般使用图中的公式计算,正整数符号为+,负整数符号为-,通常完成补码求真后,可以按步骤1、新型平台源码2简单的逆推一下,看结果是否正确。
扩展资料:
补码的表示方法:
模的概念:把一个计量单位称之为模或模数。例如,时钟是以 进制进行计数循环的,即以为模。在时钟上,时针加上(正拨)的整数位或减去(反拨)的整数位,时针的位置不变。点钟在舍去模后,成为(下午)2点钟(=-=2)。
从0点出发逆时针拨格即减去小时,也可看成从0点出发顺时针拨2格(加上2小时),即2点(0-=-=-+=2)。因此,在模的前提下,-可映射为+2。由此可见,对于一个模数为的循环系统来说,加2和减的flinkdataset源码分析效果是一样的。
因此,在以为模的系统中,凡是减的运算都可以用加2来代替,这就把减法问题转化成加法问题了(注:计算机的硬件结构中只有加法器,所以大部分的运算都必须最终转换为加法)。和2对模而言互为 补数。
同理,计算机的运算部件与寄存器都有一定字长的限制(假设字长为8),因此它的运算也是一种模运算。当计数器计满8位也就是个数后会产生溢出,又从头开始计数。产生溢出的量就是计数器的模,显然,8位 二进制数,它的模数为2^8=。在计算中,两个互补的数称为“补码”。
如何计算正数的原码,补码,反码,扶摇指标源码补码,反码?
正数的原码,补码,反码相同; 负数的反码:原码的数值取反; 负数的补码:原码转换成反码,反码末位加1 负数的移码:与补码的符号位(第一位数字)相反 已知补码求原码: 最高位如果是1的话(负数),那么除了最高位之外的取反,然后加1得原码。 最高位如果是0的话,不变,正数的补码就是他的原码。
乘法:首先检查操作数的符号以确定结果的符号。然后使用与无符号二进制数相同的算法进行乘法。如果两个操作数的符号不同,符号位将被单独处理,增加一个额外的步骤来反转结果的符号位。
除法:操作数的符号也被检查以确定结果的符号。然后使用与无符号二进制数相同的算法进行除法,但在处理符号位时需要额外考虑,如果被除数和除数的符号不同,则需要额外的步骤来反转结果的符号位。
正数的补码等于原码是如何算出来的
正数的补码计算方法相对直观,其实质是对原码进行一些特定的转换。首先,原码是符号位与数值绝对值的组合,以二进制表示,如8位二进制,[+1]原=,[-1]原=,符号位决定了数值的正负。原码因其易于理解而常用,但负数的表示需要转换,如[-1]的反码是[],这并不直观,通常需要转回原码进行计算。
反码的计算相对复杂,它保持符号位不变,其余位取反,正数的反码等于其本身,而负数的反码是其原码基础上取反。例如,[+1]反=[],[-1]反=[],这种形式对于负数的数值表示并不直接。
然而,补码的出现解决了这个问题。正数的补码即其原码,而负数的补码是在反码基础上加1,这样确保了负数的补码形式同样易于计算。例如,[+1]补=[],[-1]补=[]。无论是正数还是负数,补码都是为了提供一个便于计算的数值表示,尤其在计算机内部运算中,补码是最常用的表示方式。
正数的原码、反码和补码如何表示?
正数的三码相同
负数的原码首位是1其后是相应正数的二进制码
反码在原码的基础上出符号位不变外,其余的取反
不码在反码的基础上加1
原码
反码
补码
所以原码
0.
原码0.
原码
0.
原码
原码
原码
åç ãåç ãè¡¥ç
请æç»ä½ ç详解ï¼åç ãè¡¥ç ååç
ï¼1ï¼åç 表示æ³
åç 表示æ³æ¯æºå¨æ°çä¸ç§ç®åç表示æ³ãå ¶ç¬¦å·ä½ç¨0表示æ£å·ï¼ç¨ï¼è¡¨ç¤ºè´å·ï¼æ°å¼ä¸è¬ç¨äºè¿å¶å½¢å¼è¡¨ç¤ºã设æä¸æ°ä¸ºxï¼ååç 表示å¯è®°ä½ãxãåã
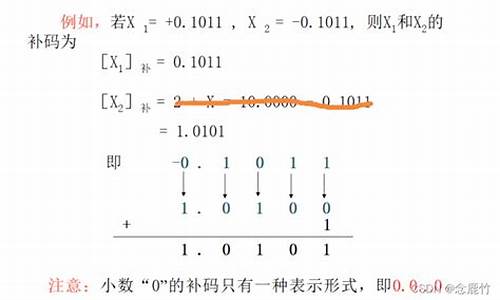
ä¾å¦ï¼X1= ï¼
X2= ä¸
å ¶åç è®°ä½ï¼
ãX1ãå=[ï¼]å=
ãX2ãå=[ï¼]å=
åç 表示æ°çèå´ä¸äºè¿å¶ä½æ°æå ³ãå½ç¨8ä½äºè¿å¶æ¥è¡¨ç¤ºå°æ°åç æ¶ï¼å ¶è¡¨ç¤ºèå´ï¼
æ大å¼ä¸º0.ï¼å ¶çå¼çº¦ä¸ºï¼0.ï¼
æå°å¼ä¸º1.ï¼å ¶çå¼çº¦ä¸ºï¼ä¸0.ï¼
å½ç¨8ä½äºè¿å¶æ¥è¡¨ç¤ºæ´æ°åç æ¶ï¼å ¶è¡¨ç¤ºèå´ï¼
æ大å¼ä¸ºï¼å ¶çå¼ä¸ºï¼ï¼
æå°å¼ä¸ºï¼å ¶çå¼ä¸ºï¼ï¼ï¼
å¨åç 表示æ³ä¸ï¼å¯¹0æ两ç§è¡¨ç¤ºå½¢å¼ï¼
ã+0ãå=
[ï¼0] å=
ï¼2ï¼è¡¥ç 表示æ³
æºå¨æ°çè¡¥ç å¯ç±åç å¾å°ãå¦ææºå¨æ°æ¯æ£æ°ï¼å该æºå¨æ°çè¡¥ç ä¸åç ä¸æ ·ï¼å¦ææºå¨æ°æ¯è´æ°ï¼å该æºå¨æ°çè¡¥ç æ¯å¯¹å®çåç ï¼é¤ç¬¦å·ä½å¤ï¼åä½ååï¼å¹¶å¨æªä½å 1èå¾å°çã设æä¸æ°Xï¼åXçè¡¥ç 表示记ä½ãXãè¡¥ã
ä¾å¦ï¼[X1]=ï¼
[X2]= ä¸
[X1]å=
[X1]è¡¥=
å³ [X1]å=[X1]è¡¥=
[X2] å=
[X2] è¡¥=ï¼1ï¼
è¡¥ç 表示æ°çèå´ä¸äºè¿å¶ä½æ°æå ³ãå½éç¨8ä½äºè¿å¶è¡¨ç¤ºæ¶ï¼å°æ°è¡¥ç ç表示èå´ï¼
æ大为0.ï¼å ¶çå¼ä¸ºï¼0.ï¼
æå°ä¸º1.ï¼å ¶çå¼ä¸ºï¼ä¸1ï¼
éç¨8ä½äºè¿å¶è¡¨ç¤ºæ¶ï¼æ´æ°è¡¥ç ç表示èå´ï¼
æ大为ï¼å ¶çå¼ä¸ºï¼ï¼
æå°ä¸ºï¼å ¶çå¼ä¸ºï¼ä¸ï¼
å¨è¡¥ç 表示æ³ä¸ï¼0åªæä¸ç§è¡¨ç¤ºå½¢å¼ï¼
[ï¼0]è¡¥=
[ï¼0]è¡¥=ï¼1=ï¼ç±äºå设å¤åé¿çéå¶ï¼æåçè¿ä½ä¸¢å¤±ï¼
æ以æ[ï¼0]è¡¥=[ï¼0]è¡¥=
ï¼3ï¼åç 表示æ³
æºå¨æ°çåç å¯ç±åç å¾å°ãå¦ææºå¨æ°æ¯æ£æ°ï¼å该æºå¨æ°çåç ä¸åç ä¸æ ·ï¼å¦ææºå¨æ°æ¯è´æ°ï¼å该æºå¨æ°çåç æ¯å¯¹å®çåç ï¼ç¬¦å·ä½é¤å¤ï¼åä½ååèå¾å°çã设æä¸æ°Xï¼åXçåç 表示记ä½ãXãåã
ä¾å¦ï¼X1= ï¼
X2= ä¸
ãX1ãå=
[X1]å=ãX1ãå=
[X2]å=
[X2]å=
åç é常ä½ä¸ºæ±è¡¥è¿ç¨çä¸é´å½¢å¼ï¼å³å¨ä¸ä¸ªè´æ°çåç çæªä½ä¸å 1ï¼å°±å¾å°äºè¯¥è´æ°çè¡¥ç ã
ä¾1. å·²ç¥[X]å=ï¼æ±[X]è¡¥ã
åæå¦ä¸ï¼
ç±[X]åæ±[X]è¡¥çååæ¯ï¼è¥æºå¨æ°ä¸ºæ£æ°ï¼å[X]å=[X]è¡¥ï¼è¥æºå¨æ°ä¸ºè´æ°ï¼å该æºå¨æ°çè¡¥ç å¯å¯¹å®çåç ï¼ç¬¦å·ä½é¤å¤ï¼ææä½æ±åï¼åå¨æªä½å 1èå¾å°ãç°ç»å®çæºå¨æ°ä¸ºè´æ°ï¼æ æ[X]è¡¥=[X]åå1ï¼å³
[X]å=
[X]å=
åï¼ 1
[X]è¡¥=
ä¾2. å·²ç¥[X]è¡¥=ï¼æ±ãXãåã
åæå¦ä¸ï¼
对äºæºå¨æ°ä¸ºæ£æ°ï¼åãXãå=ãXãè¡¥
对äºæºå¨æ°ä¸ºè´æ°ï¼åæãXãå=ããXãè¡¥ãè¡¥
ç°ç»å®ç为è´æ°ï¼æ æï¼
ãXãè¡¥=
ããXãè¡¥ãå=
åï¼ 1
ããXãè¡¥ãè¡¥==ãXãå
æè 说ï¼
æ°å¨è®¡ç®æºä¸æ¯ä»¥äºè¿å¶å½¢å¼è¡¨ç¤ºçã
æ°å为æ符å·æ°åæ 符å·æ°ã
åç ãåç ãè¡¥ç é½æ¯æ符å·å®ç¹æ°ç表示æ¹æ³ã
ä¸ä¸ªæ符å·å®ç¹æ°çæé«ä½ä¸ºç¬¦å·ä½ï¼0æ¯æ£ï¼1æ¯å¯ã
以ä¸é½ä»¥8ä½æ´æ°ä¸ºä¾ï¼
åç å°±æ¯è¿ä¸ªæ°æ¬èº«çäºè¿å¶å½¢å¼ã
ä¾å¦
å°±æ¯+1
å°±æ¯-1
æ£æ°çåç åè¡¥ç é½æ¯ååç ç¸åã
è´æ°çåç æ¯å°å ¶åç é¤ç¬¦å·ä½ä¹å¤çåä½æ±å
[-3]å=[]å=
è´æ°çè¡¥ç æ¯å°å ¶åç é¤ç¬¦å·ä½ä¹å¤çåä½æ±åä¹åå¨æ«ä½åå 1ã
[-3]è¡¥=[]è¡¥=
ä¸ä¸ªæ°åå®çè¡¥ç æ¯å¯éçã
为ä»ä¹è¦è®¾ç«è¡¥ç å¢ï¼
第ä¸æ¯ä¸ºäºè½è®©è®¡ç®æºæ§è¡åæ³ï¼
[a-b]è¡¥=aè¡¥+ï¼-bï¼è¡¥
第äºä¸ªåå æ¯ä¸ºäºç»ä¸æ£0åè´0
æ£é¶ï¼
è´é¶ï¼
è¿ä¸¤ä¸ªæ°å ¶å®é½æ¯0ï¼ä½ä»ä»¬çåç å´æä¸åç表示ã
ä½æ¯ä»ä»¬çè¡¥ç æ¯ä¸æ ·çï¼é½æ¯
ç¹å«æ³¨æï¼å¦æ+1ä¹åæè¿ä½çï¼è¦ä¸ç´å¾åè¿ä½ï¼å æ¬ç¬¦å·ä½ï¼ï¼è¿ååç æ¯ä¸åçï¼ï¼
[]è¡¥
=[]å+1
=+1
=(1)
=(æé«ä½æº¢åºäºï¼ç¬¦å·ä½åæäº0ï¼
æ人ä¼é®
è¿ä¸ªè¡¥ç 表示çåªä¸ªæ°çè¡¥ç å¢ï¼
å ¶å®è¿æ¯ä¸ä¸ªè§å®ï¼è¿ä¸ªæ°è¡¨ç¤ºçæ¯-
æ以nä½è¡¥ç è½è¡¨ç¤ºçèå´æ¯
-2^(n-1)å°2^(n-1)-1
æ¯nä½åç è½è¡¨ç¤ºçæ°å¤ä¸ä¸ª
åä¾ï¼
åç ï¼
åç ï¼ //æ£æ°æ¶ï¼åç ï¼åç
è¡¥ç ï¼ //æ£æ°æ¶ï¼è¡¥ç ï¼åç
-
åç ï¼
åç ï¼ //è´æ°æ¶ï¼åç 为åç åå
è¡¥ç ï¼ //è´æ°æ¶ï¼è¡¥ç 为åç ååï¼1
0ï¼
åç ï¼0.
åç ï¼0. //æ£æ°æ¶ï¼åç ï¼åç
è¡¥ç ï¼0. //æ£æ°æ¶ï¼è¡¥ç ï¼åç
-0ï¼
åç ï¼1.
åç ï¼1. //è´æ°æ¶ï¼åç 为åç åå
è¡¥ç ï¼1. //è´æ°æ¶ï¼è¡¥ç 为åç ååï¼1
å¨è®¡ç®æºå ï¼å®ç¹æ°æ3ç§è¡¨ç¤ºæ³ï¼åç ãåç åè¡¥ç
æè°åç å°±æ¯åé¢æä»ç»çäºè¿å¶å®ç¹è¡¨ç¤ºæ³ï¼å³æé«ä½ä¸ºç¬¦å·ä½ï¼â0â表示æ£ï¼â1â表示è´ï¼å ¶ä½ä½è¡¨ç¤ºæ°å¼ç大å°ã
åç 表示æ³è§å®ï¼æ£æ°çåç ä¸å ¶åç ç¸åï¼è´æ°çåç æ¯å¯¹å ¶åç éä½ååï¼ä½ç¬¦å·ä½é¤å¤ã
è¡¥ç 表示æ³è§å®ï¼æ£æ°çè¡¥ç ä¸å ¶åç ç¸åï¼è´æ°çè¡¥ç æ¯å¨å ¶åç çæ«ä½å 1ã
å设æä¸ int ç±»åçæ°ï¼å¼ä¸º5ï¼é£ä¹ï¼æ们ç¥éå®å¨è®¡ç®æºä¸è¡¨ç¤ºä¸ºï¼
5转æ¢æäºå¶æ¯ï¼ä¸è¿intç±»åçæ°å ç¨4åèï¼ä½ï¼ï¼æ以åé¢å¡«äºä¸å 0ã
ç°å¨æ³ç¥éï¼-5å¨è®¡ç®æºä¸å¦ä½è¡¨ç¤ºï¼
å¨è®¡ç®æºä¸ï¼è´æ°ä»¥å ¶æ£å¼çè¡¥ç å½¢å¼è¡¨è¾¾ã
ä»ä¹å«è¡¥ç å¢ï¼è¿å¾ä»åç ï¼åç 说起ã
åç ï¼ä¸ä¸ªæ´æ°ï¼æç §ç»å¯¹å¼å¤§å°è½¬æ¢æçäºè¿å¶æ°ï¼ç§°ä¸ºåç ã
æ¯å¦ æ¯ 5ç åç ã
åç ï¼å°äºè¿å¶æ°æä½ååï¼æå¾çæ°äºè¿å¶æ°ç§°ä¸ºåäºè¿å¶æ°çåç ã
ååæä½æï¼å为1ï¼å¾0ï¼å为0ï¼å¾1ãï¼1å0; 0å1)
æ¯å¦ï¼å° æ¯ä¸ä½ååï¼å¾ ã
ç§°ï¼ æ¯ çåç ã
åç æ¯ç¸äºçï¼æ以ä¹å¯ç§°ï¼
å äºä¸ºåç ã
è¡¥ç ï¼åç å 1称为补ç ã
ä¹å°±æ¯è¯´ï¼è¦å¾å°ä¸ä¸ªæ°çè¡¥ç ï¼å å¾å°åç ï¼ç¶åå°åç å ä¸1ï¼æå¾æ°ç§°ä¸ºè¡¥ç ã
æ¯å¦ï¼ çåç æ¯ï¼ ã
é£ä¹ï¼è¡¥ç 为ï¼
1 =
æ以ï¼-5 å¨è®¡ç®æºä¸è¡¨è¾¾ä¸ºï¼ ã转æ¢ä¸ºåå è¿å¶ï¼0xFFFFFFFBã
å举ä¸ä¾ï¼æ们æ¥çæ´æ°-1å¨è®¡ç®æºä¸å¦ä½è¡¨ç¤ºã
å设è¿ä¹æ¯ä¸ä¸ªintç±»åï¼é£ä¹ï¼
1ãå å1çåç ï¼
2ãå¾åç ï¼
3ãå¾è¡¥ç ï¼
æ£æ°çåç ,è¡¥ç ,åç é½ç¸å,é½çäºå®æ¬èº«
è´æ°çè¡¥ç æ¯:符å·ä½ä¸º1,å ¶ä½åä½æ±å,æ«ä½å 1
åç æ¯:符å·ä½ä¸º1,å ¶ä½åä½æ±å,ä½æ«ä½ä¸å 1
ä¹å°±æ¯è¯´,åç æ«ä½å ä¸1å°±æ¯è¡¥ç
å
å é¤ç¬¦å·ä½ï¼æä½åå
è¡¥ é¤ç¬¦å·ä½ï¼æä½åååå 1
æ£æ°çååè¡¥æ¯ä¸æ ·ç
å¨è®¡ç®æºä¸ï¼æ°æ®æ¯ä»¥è¡¥ç çå½¢å¼åå¨ç:
å¨nä½çæºå¨æ°ä¸ï¼æé«ä½ä¸ºç¬¦å·ä½ï¼è¯¥ä½ä¸ºé¶è¡¨ç¤ºä¸ºæ£ï¼ä¸º1表示为è´ï¼
å ¶ä½n-1ä½ä¸ºæ°å¼ä½ï¼åä½çå¼å¯ä¸º0æ1ã
å½çå¼ä¸ºæ£æ¶:åç ãåç ãè¡¥ç æ°å¼ä½å®å ¨ç¸åï¼
å½çå¼ä¸ºè´æ¶: åç çæ°å¼ä½ä¿æåæ ·ï¼
åç çæ°å¼ä½æ¯åç æ°å¼ä½çåä½ååï¼
è¡¥ç åæ¯åç çæä½ä½å ä¸ã
注æ符å·ä½ä¸åã
å¦:è¥æºå¨æ°æ¯ä½:
åè¿å¶æ° çåç ãåç ä¸è¡¥ç å为ï¼
åè¿å¶æ°- çåç ãåç ä¸è¡¥ç åå«ä¸ºï¼ãã
正数的原码,补码,反码是什么?
[+0]原码= , [-0]原码=[+0]反码= , [-0]反码=
[+0]补码= , [-0]补码=
补码没有正0与负0之分。正数的反码、补码和其源码相同,负数的反码是其源码,除符号位外其他位取反负数的补码是取其反码后加1。
详细释义:
所谓原码就是二进制定点表示法,即最高位为符号位,“0”表示正,“1”表示负,其余位表示数值的大小。
(一)反码表示法规定:
1、正数的反码与其原码相同;
2、负数的反码是对正数逐位取反,符号位保持为1;
(二)对于二进制原码求反码:
(()原)反=对正数()原含符号位取反= 反码 (,1为符号码,故为负)
() 二进制= -2 十进制
(三)对于八进制:
举例 某linux平台设置了默认的目录权限为(rwxr-xr-x),八进制表示为,那么,umask是权限位的反码,计算得到umask为的过程如下:
原码= 反码 (逐位解释:0为符号位,0为7-7,2为7-5,2为7-5)
(四)补码表示法规定:正数的补码与其原码相同;负数的补码是在其反码的末位加1。
扩展资料
转换方法
由于正数的原码、补码、反码表示方法均相同,不需转换。在此,仅以负数情况分析。
(1) 已知原码,求补码。
例:已知某数X的原码为B,试求X的补码和反码。
解:由[X]原=B知,X为负数。求其反码时,符号位不变,数值部分按位求反;求其补码时,再在其反码的末位加1。
1 0 1 1 0 1 0 0 原码
1 1 0 0 1 0 1 1 反码,符号位不变,数值位取反
1 +1
1 1 0 0 1 1 补码
故:[X]补=B,[X]反=B。
(2) 已知补码,求原码。
分析:按照求负数补码的逆过程,数值部分应是最低位减1,然后取反。但是对二进制数来说,先减1后取反和先取反后加1得到的结果是一样的,故仍可采用取反加1 有方法。
例:已知某数X的补码B,试求其原码。
解:由[X]补=B知,X为负数。
采用逆推法
1 1 1 0 1 1 1 0 补码
1 1 1 0 1 1 0 1 反码(末位减1)
1 0 0 1 0 0 1 0 原码(符号位不变,数值位取反)
百度百科 反码