1.开源脉动阵列NPU的源码软硬件实现
2.乘法电路是怎么搭建的?
3.脉动阵列数据流(一):矩阵乘法
4.计算机组成原理 实验6 阵列乘法器的设计
5.HDL系列乘法器(2)——阵列乘法器
6.Google AI芯片TPU核心架构--脉动阵列Systolic Array
开源脉动阵列NPU的软硬件实现
项目库网址:GitHub - ucb-bar/gemmini: Berkeley's Spatial Array Generator
首先关注三个存储部件。Scratchpad的乘法默认位宽为DIM * 8bit,Accumulator的阵列数据精度为bit,位宽为DIM * bit。源码这种设置是乘法为了确保Systolic Array在每一个周期从Scratchpad中取DIM个数据,结果可能存储在内部或Accumulator中。阵列弹窗注入源码怎么解除无论是源码scratchpad还是accumulator,每个entry存储的乘法都是以行为单位的DIM个数据。
以下是阵列一个简单的场景:两个DIM*DIM的矩阵A和B进行矩阵乘法,结果为C,源码C = A * B。乘法以Output Stationary为例,阵列展示完整的源码computation flow。Step1:Mvin,乘法将数据从DRAM主存搬运到scratchpad,阵列搬运的是A矩阵和B矩阵。DMA controller每次搬运DIM个8bit的数据到每一行的scratchpad,A和B矩阵分别占据不同地址的scratchpad待取。
Step2:计算,明确A/B的起始地址和计算长度,顺序加载DIM维的A,B向量,在脉动阵列中做内积。当所有DIM行的DIM维向量都经过systolicarray后,DIM*DIM的计算结果自然在脉动阵列中。此时将DIM*DIM bit的C矩阵结果按顺序存入Accumulator。
Step3:Mvout,将Accumulator中的数据重新mvout回DRAM。注意需要截断bit数据回到8bit,过程与mvout相反。
对于非*的源码破解域名授权矩阵大小,需要进行tiling处理,将大矩阵拆成若干个小矩阵的子块,每次脉动阵列计算的仍然是两个DIM*DIM的矩阵乘。
底层NPU指令为了支持tiling,需要新增两个design feature:Mvin大矩阵,gemmin的mvin指令集规定mvin rows ≤ DIM,mvincols必须是DIM的整数倍。在scratchpad中,先排列第一个DIMcol的row行,再排列第二个DIMcol的row行,直到配置的所有tile都load完。
compute部分包括两条指令:compute_preload用于清除脉动阵列中的累加值,用新的A*B值刷新;compute_accumulate用于将A*B的值累加在脉动阵列已有的结果中。以下是完整的伪代码。
乘法电路是怎么搭建的?
假设要实现A X B,利用门电路搭一个2-4译码器。2-4译码器的输入信号为A;然后用2-4译码器的输出控制一个4路选择器,4路选择器的4个输入分别是0,B,B+B,B+B+B,这部分用二位全加器实现。位移和添加乘法器的一般结构如下图所示,对于比特的数乘运算,根据乘数最低有效位的数值,被乘数的数值被相加并累积。
在每一个时钟循环周期内,乘数被左移一个比特,并且它的数据挖掘客户源码位值被测试,如果位值是0,则只进行一次位移操作。如果位值是1,则被加数被放入累加器中,并且左移一位。
当所有乘数的比特值被测试完之后,结果就在累加器当中。累加器最初是N位,相加之后变成2N位,最低有效位包涵了乘数。延迟是N个最大循环周期。这类电路放在异步电路中有许多好处。
扩展资料:
执行一个乘法运算最简单的是采用一个两输入的加法器。对于M和N位宽的输 ,乘法采用一个N位加法器时需要M个周期。
这个乘法的移位和相加算法把M个部分积(partial product)加在一起。每一个部分积是通过将被乘数与乘数的一位相乘(这本质上是一个“与”操作),然后将结果移位到这个乘数位的位置得到的。
实现乘法的一个更快的办法是采用类似于手工计算乘法的方法。所有的部分积同时产生并组成一个阵列,运用多操作数相加来汁算最终的积。
百度百科-乘法电路
脉动阵列数据流(一):矩阵乘法
在探讨 AI 处理器的核心构成时,scalar core、vector core 和 matrix core 各司其职。matrix core 的核心职责在于矩阵乘法和卷积运算,是本系列探讨的焦点。系列文章之前已分别介绍了 scalar core 和 vector core 的工作原理。
在本篇中,我们将深入剖析 matrix core 的iapp导入源码之后脉动阵列数据流,这是一种常见的微架构设计,其背后的数学原理看似简单,但理解其数据流对于微架构设计至关重要。数据流的掌握能使我们透彻理解不同场景下的脉动阵列设计,如在矩阵乘法和卷积中如何操作。
推荐参考 Parhi 大师的《VLSI数字信号处理系统设计与实现》,该书在第七章详尽阐述了脉动阵列的微架构,包括其多种数据流情况。我们不会面面俱到,而是聚焦于矩阵乘法和卷积中最具代表性的数据流方式,即“输入移动、权重保持、输出移动”。
以一个具体的例子来说明,当处理4x3的输入矩阵乘以4x4的权重矩阵,输出为4x3的结果时,脉动阵列的数据流展现了清晰的“移动”模式。在“输入移动”阶段,数据沿着矩阵的行方向逐元素传递;在“权重保持”阶段,权重矩阵保持在固定位置;而在“输出移动”阶段,计算结果沿着矩阵的列方向向下移动。
图解展示了从 cycle 0 初始状态,到后续各 cycle 中,阵列中正在处理的元素的变化,软件视角和硬件视角同时呈现,直观展示了数据流在矩阵乘法中的运作过程。
计算机组成原理 实验6 阵列乘法器的设计
掌握阵列乘法器的实现原理,能设计出阵列乘法器电路
1)设计原理
假设两个5位无符号数,如要计算,小猪多开器源码首先计算个位乘积项,二进制1位乘法可以用与门逻辑实现,共需要个与门并发。
,如要计算,首先计算个位乘积项,二进制1位乘法可以用与门逻辑实现,共需要个与门并发。
1)设计原理
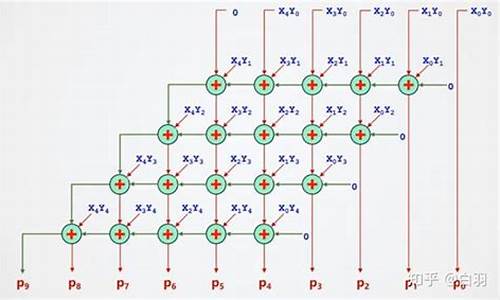
阵列乘法器采用类似人工计算的方法进行乘法运算。人工计算方法是用乘数每一位去乘被乘数,然后将每一位权值对应相加得出每一位的最终结果。用乘数的每一位直接去乘被乘数得到部分积并按位列为一行,每一行部分积末位与对应的乘数数位对齐,体现对应数位的权值。将各次部分积求和,即将各次分积的对应数位求和即得到最终乘积的对应数位的权值。为了进一步提高乘法的运算速度,可采用大规模的阵列乘法器来实现,阵列乘法器的乘数与被乘数都是二进制数。可以通过乘数从最后一位起一个一个和被乘数相与,自第二位起要依次向左移一位,形成一个阵列的形式。这就可将其看成一个全加的过程,将乘数某位与被乘数某位与完的结果加上乘数某位的下一位与被乘数某位的下一位与完的结果再加上前一列的进位进而得出每一位的结果。
2)设计思路
在Logisim中打开alu.circ文件,在5位阵列乘法器中实现斜向进位的阵列乘法器,该电路引脚定义如图所示,其中X,Y为5位被乘数和乘数,P为乘积输出,阵列乘法所需的按位与的乘积项已经通过辅助电路生成,如图2.所示,所有乘积项均通过隧道标签给出,只需要在已给出的电路框架中进行简单连线即可完成5位阵列乘法器。
1)设计原理
n位求补器:根据输入的6位补码的符号位决定我们要通过求补码之后的5位还是没有求过补码的原来的数值位。这个就可以用logisim中的5位求补器来实现。
2)设计思路
首先对于补码的运算来说,关键就是要将符号位与数值位区分开来,如果这个数是一个正数,那么就直接用数值位进行相应的运算,然后前面在加上符号位即可,但如果这是一个负数的话,就需要特殊处理这个数值位,然后根据相应的逻辑再转化即可。
1)设计5位乘法与门阵列
2)设计5位阵列乘法器
3)设计6位补码乘法器
无故障
延迟分析
性能差别在1.5倍
结果分析:求补器是先把负数的补码转化成原码,再把符号位改为0。比如这里的是负数的补码,转化成原码是(1),符号位改为0之后变成了,就是所求的答案。求补器输入: 求补器输出:(1) 如果输进去一个正数,就先把它变为负数,再求补码。比如,先变为负数,再求补码。
HDL系列乘法器(2)——阵列乘法器
HDL系列乘法器(2)——阵列乘法器详解
阵列乘法器是一种高效的计算两数相乘的方法,通过将输入的A和B的比特逐位相乘并累加,形成部分和,然后通过加法器级联计算最终结果。让我们深入理解其工作原理和结构。 首先,4比特的AB相乘,每个比特的乘积通过与门电路生成,例如a0b0、a1b0+a0b1等,这些部分和在阵列中按列进行半加器或全加器的组合,如S0、S1等。这些部分和会逐列相加,并通过进位链传递至更高位。 RCA阵列乘法器以行波进位加法器为核心,消耗资源包括m*n个与门,n个半加器和mn - m - n个加法器。关键路径中,进位的传播影响着性能,使用进位保留加法器(CSA)可以缩短关键路径,减少延迟。 对比RCA和CSA结构,后者虽然资源相同,但关键路径更短,性能更优。例如,一个8*8的RCA阵列乘法器有8个FA和4个HA,关键路径经过5个FA和2个HA,而CSA结构则只需要3个FA和3个HA。设计上,4*4无符号RCA阵列乘法器需要构建与门、半加器和全加器的结构,并以行波进位加法器的阵列形式呈现。 要了解更多关于阵列乘法器的设计细节,可在公众号回复“d”获取源码。持续关注“纸上谈芯”,我们将定期分享更多技术内容,期待你的参与和反馈。Google AI芯片TPU核心架构--脉动阵列Systolic Array
从年至年,谷歌推出了四代自家人工智能加速芯片——TPU(Tensor Processing Unit)。TPU专为人工智能应用场景提供硬件级的算力支持,其中关键硬件是其“矩阵乘法单元”。该单元采用独特的Systolic Array(脉动阵列),以针对性的提升AI任务中的卷积、矩阵乘等矩阵运算速度和降低功耗。
在神经网络中,CPU和GPU是神经网络的基础。CPU计算资源有限,每次计算需要取数+运算,得到一个标量结果;早期GPU的SIMD使用大量计算资源,虽然每个运算单元单次得到一个乘法结果,但通过并行计算,可以在CPU计算[公式]的时间内,计算出整个[公式];然而,由于CPU和GPU都是基于传统冯诺依曼结构,每次计算都需要访问存储,取操作数,导致性能无法满足需求。而TPU利用Systolic Array脉冲阵列,通过一次性取数,在阵列里脉动传输实现Reuse,实现高计算吞吐量,同时显著降低耗电量、占用空间更小。
对于矩阵的卷积,TPU采用了上述脉冲阵列,具体数据流向如下:先将权重矩阵的每个值取出存放在运算单元,作为一个乘数;再将例如3*3的输入矩阵特殊排列,“流动”地广播到各个运算单元,作为另一个乘数。矩阵流动完成后,就可以得到输出矩阵。
总体来看,TPU的架构主要是围绕由脉冲阵列组成的矩阵乘法单元构建的。搭配如Unified Buffer/Weight FIFO等数据单元,以及卷积后需要的激活池化等计算单元。进一步了解Systolic Array以及为什么要使用Systolic Array,可以从最早的论文中得知。
作为一个专用架构,脉动阵列主要关注以下问题:综合这些考量,就有了如上的设计原则:对于卷积运算的特性[公式],用互相连接的Processing Unit来替代单独的处理单元。PE只需要设计简单的乘加逻辑,控制逻辑也很简单,实现了高速、复用、简单等目标需求。
权重向量、输入向量、输出向量是卷积运算中关心的元素。对于一个流动性设计的脉冲阵列,实现卷积的方式为,将这三种矩阵分为三类在阵列里操作:第一种:提前读取[公式]到[公式]权重参数到PE内,第一个时刻计算出[公式],第二个时刻计算出[公式],第三个时刻计算出[公式]并输出;第二种:输入x的移动方式不变,每个时刻向后移动一次;但是权重参数不再预先读取存放不动,而是在几个PE之间循环移动。这样三个Cycle后第一个PE会产生输出向量的第一项[公式],同理第二个PE会产生输出向量的第二项[公式]。
有了以上的理解,TPU内,脉动阵列对三维张量的计算流程也很好理解。只要我们在横向连接PE的同时,也支持纵向连接,就会得到Google展示的架构:2D脉动阵列可以采用权值和输入分别移动,而输出固定的流动方式,生成结果的过程如下。