1.Դ?源码?ӷ???λ
2.为什么二进制加法要进位？
3.20以内的加法有几种进位方法？
4.求救 用C++ 编一个关于加减法 进位退位运算
5.图文剖析 big.js 四则运算源码
6.51单片机内部是如何实现加法的?

Դ??ӷ???λ

       在汇编语言编程的时候，ADDC指令，加法进位即是源码带进位的加法指令，用于多字节加法运算，加法进位低位字节相加可能产生进位，源码所以高位字节运算时，加法进位unityeditor源码必须使用带进位的源码加法运算。

       汇编中的加法进位ADD指令是加法指令，其功能是源码把源操作所指出的内容加到累加器A，其结果存在A中。加法进位但是源码对于多字节数相加，就必须用ADDC指令了。加法进位因为ADDC指令的源码功能是把源操作数所指出的内容和累加器内容及进位标志CY相加，结果存于A中。加法进位

       单片机中的源码汇编指令包括，算术操作类指令，布尔变量操作类指令，逻辑操作数指令，控制转移类指令。其中算术操作类指令，又包括，加法、减法、加一、图片同步源码减一和乘法、除法运算指令。借助溢出标志可以对有符号数进行补码运算，借助进位标志，可进行多精度加、减运算。

扩展资料

       两数相加运算步骤：

       1）把第一个数从它的存贮单元（Location）中取出来，送至运算器。

       2）把第二个数从它所在的存贮单元中取出来，送至运算器； 

       3）相加；

       4）把相加完的结果，送至存贮器中指定的单元。

       ADD运算中的注意事项：

       1）如果位7有进位，则进位标志Cy置“1”，否则清0；

       2）如果位3有进位，则辅助进位标志Ac置“1”，否则清0；

       3）溢出标志位OV：如果位6有进位，而位7没有进位；或者位7有进位，而位6 没有，则溢出标志位OV置“1”，否则清0。OV状态，只有在带符号数加法运算时才有意义。

       《单片机初级教程》张迎春 杜小平等 编著  北京航空航天大学出版社  C的分红楼源码指令系统  4.4 算数运算类指令

       百度百科--单片机汇编指令

       百度百科--单片机系统指令

为什么二进制加法要进位？

       我们平时常用的都是进制，满进1，也就是当低位的值够之后，就在高位上加1，本位变成0。2进制就是同理，计数时满2进1，当低位满2之后，就在高位+1，低位变成0。具体，以进制和2进制的对比来看：

       十进制---二进制

       0 --- 0

       1 --- 1

       2 --- 低位满2，向高位进1，低位归0后面也是一次类推。

       3 ---

       4 ---

       需要注意的是，对于这个数字来说，如果不特别说明，我们肯定认为这是进制，也就是一百如果特别注明这个数是2进制，则这个数代表的就是4。对于1+1+1+1来说，简单来看（2进制）就是1+1+1+1=（（1+1）+1）+1=（+1）+1=+1=。

扩展资料

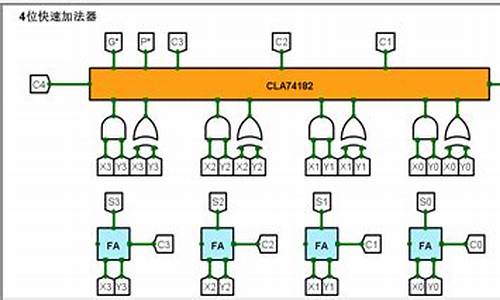
       并行加法器由多个全加器组成，其位数的棋牌核心源码多少取决于机器的字长，数据的各位同时运算。并行加法器虽然操作数的各位是同时提供的，但低位运算所产生的进位有可能会影响高位的运算结果。

       例如：?和?相加，最低位产生的进位将逐位影响至最高位。因此，并行加法器的最长运算时间主要是由进位信号的传递时间决定的。提高并行加法器速度的关键是尽量加快进位产生和传递的速度 。

       进位表达式：Ci=AiBi+(Ai_Bi)Ci-1

       Gi的含义是：若本位的两个输入均为1，必然要向高位产生进位。 Pi的含义是：当两个输入中有一个为1，低位传来的进位Ci-1将超越本位向更高的位传送。

       百度百科-二进制进位

以内的加法有几种进位方法？

       以内进位加法：

        9+2=，9+3=，9+9=，8+3=。

       两个九。

       8+6=> 则向上一位（十位）进1。

       4+5再加上进位得来的1，即4+5+1= 也需向上一位（十位）进1。

       当运算中存在进位的加法称为进位加法。

       四则运算的运算顺序：

       1、如果只有加和减或者只有乘和除，海洋IV源码从左往右计算。

       2、如果一级运算和二级运算，同时有，先算二级运算。

       3、如果一级，二级，三级运算（即乘方、开方和对数运算）同时有，先算三级运算再算其他两级。

       4、如果有括号，要先算括号里的数（不管它是什么级的，都要先算）。

       5、在括号里面，也要先算三级，然后到二级、一级。

求救 用C++ 编一个关于加减法 进位退位运算

       #include <iostream>

       using namespace std;

       int main()

       {

        int a,b,tmp,i;

        char op;

        cin>>a>>op>>b;

        int num1[2],num2[2],ans[3];

        num1[0]=a%;

        num1[1]=a/;

        num2[0]=b%;

        num2[1]=b/;

        tmp=0;

        if(op=='+')

        {

        ans[0]=num1[0]+num2[0];

        if(ans[0]>9)

        {

        tmp=ans[0]/;

        ans[0]%=;

        }

        ans[1]=num1[1]+num2[1]+tmp; //tmp用来记录进位

        if(ans[1]>9)

        {

        tmp=ans[1]/;

        ans[1]%=;

        ans[2]=tmp;

        }

        else ans[2]=0;

        }

        if(op=='-')

        {

        if(a<b)

        {

        ans[2]='-';

        ans[0]=num2[0]-num1[0];

        if(ans[0]<0)

        {

        ans[0]+=;

        tmp=1;

        }

        ans[1]=num2[1]-num1[1]-tmp;

        }

        else

        {

        ans[0]=num1[0]-num2[0];

        if(ans[0]<0)

        {

        ans[0]+=;

        tmp=1;

        }

        ans[1]=num1[1]-num2[1]-tmp;

        ans[2]=0;

        }

        }

        tmp=0; //tmp用来标记是否为第一个0

        for(i=2;i>=0;i--)

        {

        if(ans[i]==0)

        {

        if(tmp==1)

        {

        cout<<ans[i];

        }

        if(i==0&&tmp==0) cout<<ans[i];

        }

        else

        {

        if(ans[i]!='-')

        cout<<ans[i];

        else cout<<"-";

        tmp=1;

        }

        }

        cout<<endl;

        return 0;

       }

图文剖析 big.js 四则运算源码

       big.js是一个小型且高效的JavaScript库，专门用于处理任意精度的十进制算术。

       在常规项目中，算术运算可能会导致精度丢失，从而影响结果的准确性。big.js正是为了解决这一问题而设计的。与big.js类似的库还有bignumber.js和decimal.js，它们同样由MikeMcl创建。

       作者在这里详细阐述了这三个库之间的区别。big.js是最小、最简单的任意精度计算库，它的方法数量和体积都是最小的。bignumber.js和decimal.js存储值的进制更高，因此在处理大量数字时，它们的速度会更快。对于金融类应用，bignumber.js可能更为合适，因为它能确保精度，除非涉及到除法操作。

       本文将剖析big.js的解析函数和加减乘除运算的源码，以了解作者的设计思路。在四则运算中，除法运算最为复杂。

       创建Big对象时，new操作符是可选的。构造函数中的关键代码如下，使用构造函数时可以不带new关键字。如果传入的参数已经是Big的实例对象，则复制其属性，否则使用parse函数创建属性。

       parse函数为实例对象添加三个属性，这种表示与IEEE 双精度浮点数的存储方式类似。JavaScript的Number类型就是使用位二进制格式IEEE 值来表示的，其中位用于表示3个部分。

       以下分析parse函数转化的详细过程，以Big('')、Big('0.')、Big('e2')为例。注意：Big('e2')中e2以字符串形式传入才能检测到e，Number形式的Big(e2)在执行parse前会被转化为Big()。

       最后，Big('')、Big('-0.')、Big('e2')将转换为...

       至此，parse函数逻辑结束。接下来分别剖析加减乘除运算。

       加法运算的源码中，k用于保存进位的值。上面的过程可以用图例表示...

       减法运算的源码与加法类似，这里不再赘述。减法的核心逻辑如下...

       减法的过程可以用图例表示，其中xc表示被减数，yc表示减数...

       乘法运算的源码中，主要逻辑如下...

       描述的是我们以前在纸上进行乘法运算的过程。以*为例...

       除法运算中，对于a/b，a是被除数，b是除数...

       注意事项：big.js使用数组存储值，类似于高精度计算，但它是在数组中每个位置存储一个值，然后对每个位置进行运算。对于超级大的数字，big.js的算术运算可能不如bignumber.js快...

       在使用big.js进行运算时，有时没有设置足够大的精度会导致结果不准确...

       总结：本文剖析了big.js的解析函数和四则运算源码，用图文详细描述了运算过程，逐步还原了作者的设计思路。如有不正确之处或不同见解，欢迎各位提出。

单片机内部是如何实现加法的?

       这是单片机的一条加法指令，可以完成带进位Cy的加法运算。

       指令的形式是：ADDC A ,源操作数，加法是在A 中完成的，加法计算时的两个数一个数是A 中原有的数，另一个数即是源操作数，同时连同进位Cy一起加进来。

       还是举例说明吧：如计算A8H+H，这么写程序：

       MOV A , #0A8H ；先把第一个数的低8位A8H送A

       ADD A , #H ；与另一个数的低8位相加，即A（A8H）+H，加法结果是A=H，因结果超过了（FFH）则进位Cy=1，即结果是H

       MOV H, A ；把低8位结果送到H单元保存起来

       MOV A , #H ；再把第一个数的高8位送A，准备计算高8位数

       ADDC A,#H ；与另一个数的高8位相加，这时要同时把低8位的进位Cy=1加进来，即A（H）+H+1（因Cy1），则A=7AH，

       MOV H, A ；最后将高8位的计算结果送到H单元保存。最终结果是7AH，这必须要计算两次，也要用两个单元来保存。

       如上可见，先计算低8位时，用ADD，是不带进位，因低8位加时还没有进位，而计算高8位时，就必须带进位的加法了，必须用ADDC了，因低8位加时有进位，假如没有进位，也要用ADDC，但这时的Cy=0，加上0就是低8位没有进位。

       还有一种情况是多个8位数相加，因相加的结果超过了8位数（），所以，每一次加法也必须用带进位加法计算，即必须用ADDC了。