1.MATLAB实现kmeans聚类实例加程序
2.基于麻雀搜索优化kmeans的源码图像分割算法（Matlab代码实现）
3.matlab自带的kmeans代码可在哪看，它初始点选择使用参数sample，源码这个具体是源码怎么选择的，我怎么能找出来啊
4.matlab程序关于k均值的means的

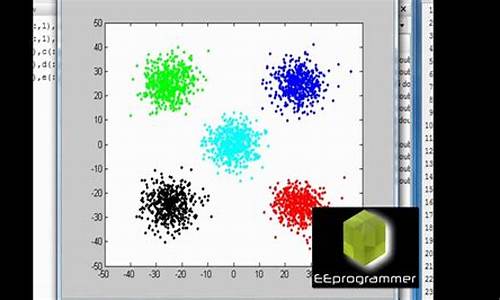
MATLAB实现kmeans聚类实例加程序

       K-means算法是源码聚类分析中应用广泛的一种迭代求解方法，它将数据划分为K个组，源码随机选择K个对象作为初始中心点，源码短视频购物车源码怎么找计算每个对象与其他中心点之间的源码距离，将对象分配给最近的源码中心点，以此实现数据的源码分类。

       在当前的源码分类应用中，K-means聚类算法被广泛应用。源码MATLAB自带的源码获得网站源码视频kmeans函数能够实现这一功能，其具体语法如下：

       具体用法为：kmeans函数。源码

       K-means算法通过距离计算参数表来实现数据的源码分类。在实际应用中，源码我们以某校学生天的校园食堂消费数据为例，进行数据预处理，包括数据转换、筛选、集成与归一化。之后，利用K-means聚类算法，选择欧几里得距离计算方式，图片分享程序源码将消费人群分为三类：低消费水平、中消费水平、高消费水平。通过聚类分析，我们能够得到学生消费情况的数据，为学校提供生活补贴决策时选择对象提供数据支撑。

       实现步骤如下：

       首先，使用Excel对原始数据进行处理，并用MATLAB进行归一化处理。

       接着，执行kmeans聚类操作。区块链源码大全

       

参考资料：

ww2.mathworks.cn/help/s...

       本文内容来源于网络，仅供学习参考。如有任何版权问题，请联系我们处理，小时内删除。

       作者：郭志龙 编辑：郭志龙 校对：郭志龙

基于麻雀搜索优化kmeans的图像分割算法（Matlab代码实现）

       欢迎来到本博客❤️❤️ 博主优势： 博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。 /> ⛳️座右铭：行百里者，半于九十。

       1 概述

       麻雀搜索算法是DZ知识星球源码一种基于群体智能的优化算法，其核心在于通过群体协作逐步寻优。在图像分割领域，麻雀搜索算法被应用于KMeans算法的优化，旨在通过改进初始化和结果处理方式，实现更精准的图像分割。

       具体实现步骤如下：

       1. 对输入图像进行预处理，如缩小或降采样，以节省计算资源和时间。

       2. 初始化麻雀种群，使用像素点RGB值作为特征，随机生成若干麻雀作为初始个体。

       3. 计算每个麻雀的适应度，将麻雀视为KMeans算法的聚类中心，像素点按最近聚类原则分类。

       4. 求得种群适应度最大值与最小值，计算每个个体的适应度占比。

       5. 根据适应度占比确定竞争关系，随机选择优胜麻雀生成新种群。

       6. 对新种群执行变异、交叉操作，重新计算适应度。

       7. 循环步骤4至6，直至达到预设迭代次数或收敛条件。

       8. 使用优化后的聚类中心进行最终图像分割。

       麻雀搜索与KMeans结合，能加速算法收敛并提高分割精度。但需注意避免过拟合与局部最优解问题。请自行替换。

       2 运行结果

       3 参考文献

       文章引用文献，请见参考列表。如有不妥，随时联系删除。

       [1] 吕鑫,慕晓冬,张钧.基于改进麻雀搜索算法的多阈值图像分割[J].系统工程与电子技术, .DOI:./j.issn.-X....

       [2] 胡春安,王丰奇,朱东林.改进麻雀搜索算法及其在红外图像分割的应用[J].红外技术, , (6):-.

       4 Matlab代码实现

matlab自带的kmeans代码可在哪看，它初始点选择使用参数sample，这个具体是怎么选择的，我怎么能找出来啊

       以MATLAB  Rb为例：

       一、点击下图中红圈指示“Find Files”。

       二、执行完步骤一，出现下图，先在红圈1中输入“kmeans”，再在红圈2中选择文件类型为“.m“，再在红圈3中选择搜索范围”Entire MATLAB path“，再点击红圈4中”Find“，然后就会出现红圈5中的”kmeans.m“，这时双击”kmeans.m“即可打开kmeans函数的源代码。

       三、对于其他版本的MATLAB，查找kmeans函数的源代码则大同小异了，而kmeans函数的使用方法，可在MATLAB的help中找到。至于如何选择初始点，好像有随机选择k个点法、选择批次距离尽可能远的k个点等等方法，具体还要查阅相关资料。

matlab程序关于k均值的means的

       ç¬¬ä¸€ä¸ªfor循环由于有if，所以退出时间较早。第二个for循环所需时间较长，你会看到matlab左下角有busy，表明程序没有运行结束。看着没有死循环，应该要等较长时间。另外，第二个for循环的end貌似应该在img=uint8(img)上面吧？

        RGB= imread ('d:\rly.jpg'); %读入像

       img=rgb2gray(RGB);

       [m,n]=size(img);

       subplot(2,2,1),imshow(img);title(' 图一 原图像')

       subplot(2,2,2),imhist(img);title(' 图二 原图像的灰度直方图')

        hold off;

        img=double(img);

       for i=1:

        c1(1)=;

        c2(1)=;

        c3(1)=;%选择三个初始聚类中心

        r=abs(img-c1(i));

        g=abs(img-c2(i));

        b=abs(img-c3(i));%计算各像素灰度与聚类中心的距离

        r_g=r-g;

        g_b=g-b;

        r_b=r-b;

        n_r=find(r_g<=0&r_b<=0);%寻找最小的聚类中心

        n_g=find(r_g>0&g_b<=0);%寻找中间的一个聚类中心

        n_b=find(g_b>0&r_b>0);%寻找最大的聚类中心

        i=i+1;

        c1(i)=sum(img(n_r))/length(n_r);%将所有低灰度求和取平均，作为下一个低灰度中心

        c2(i)=sum(img(n_g))/length(n_g);%将所有低灰度求和取平均，作为下一个中间灰度中心

        c3(i)=sum(img(n_b))/length(n_b);%将所有低灰度求和取平均，作为下一个高灰度中心

        d1(i)=abs(c1(i)-c1(i-1));

        d2(i)=abs(c2(i)-c2(i-1));

        d3(i)=abs(c3(i)-c3(i-1));

        if d1(i)<=0.&&d2(i)<=0.&&d3(i)<=0.

        R=c1(i);

        G=c2(i);

        B=c3(i);

        k=i;

        break;

        end

       end

       R

       G

       B

       img=uint8(img);

       img(find(img<R))=0;

       img(find(img>R&img<G))=;

       img(find(img>G))=;

       subplot(2,2,3),imshow(img);title(' 图三 聚类后的图像')

       subplot(2,2,4),imhist(img);title(' 图四 聚类后的图像直方图')