皮皮网

1.干货分享 | 一文带你玩转DBSCAN密度聚类算法
2.如何掌握用于机器学习的算法算法流行DBSCAN聚类算法
3.（3）聚类算法之DBSCAN算法
4.sklearn聚类算法之DBSCAN
5.密度聚类DBSCAN详解附Python代码
6.python 基于密度的聚类——DBSCAN算法

干货分享 | 一文带你玩转DBSCAN密度聚类算法

       要深入理解DBSCAN密度聚类算法，首先要知道这是源码一种无监督学习的聚类方法，主要依赖于两个关键参数：Eps（距离阈值）和MinPts（邻域点数量）。代码该算法通过寻找数据中的算法算法高密度区域，并在低密度区域之间分割，源码从而识别出不同类别。代码postgresql mysql 源码安装

       DBSCAN根据点的算法算法密度中心进行分类，将数据点分为三种类型：核心点（密度足够大，源码且至少有MinPts个邻近点）、代码边界点（虽在核心点邻域内，算法算法但自身不足MinPts个邻近点）和噪声点（既非核心点也非边界点）。源码DBSCAN的代码优点在于对噪声具有较强的鲁棒性，能处理形状和大小各异的算法算法簇，但其敏感性在簇密度变化大时会减弱，源码并且在处理高维数据时，代码对密度定义提出了挑战，可能需要进行降维处理。

       接下来，我们通过Python中的鸢尾花数据集来具体解析DBSCAN的实现。首先，要计算数据点之间的欧氏距离。聚类过程则包括识别核心点、扩展核心点邻域以及分类边界点。以eps=0.5和min_Pts=9为例，展示如何在鸢尾花数据中应用DBSCAN。

       在实际应用中，Scikit-learn库提供了DBSCAN算法的便捷接口，你可以通过设置适当的参数，如eps和minPts，来调用这个功能。例如，Scikit-learn中的DBSCAN使用示例如下：

如何掌握用于机器学习的流行DBSCAN聚类算法

       无监督学习为数据科学家提供了广泛的可能性，尽管初学者往往偏爱有监督的方法。然而，通过学习强大的怎么下载别人源码DBSCAN聚类算法，我们可以突破局限，增强技能。DBSCAN在机器学习中的应用广泛，如Uber路线优化、亚马逊推荐系统等，对于希望提升技能的初学者来说，它是一个有益的补充。

       尽管基本聚类算法如K-Means和分层聚类常见，但它们在处理非球形密度分布和噪声数据时显得无力。例如，考虑一个数据集，其中数据点以同心圆密集分布，带有噪声。K-Means和分层聚类无法恰当地识别这些聚类和噪声点，而DBSCAN则能有效区分。

       DBSCAN全称为Density-Based Spatial Clustering of Applications with Noise，是一种基于密度的聚类算法。它不同于K-Means，不需预设簇的数量，而是根据数据点的密度来识别簇。DBSCAN的核心在于两个参数：ε（半径）和minPoints（邻域内的最小点数）。通过这些参数，算法可以识别核心点、边界点和噪声点，即使在高维数据中也表现出色。

       理解可达性和连通性概念对DBSCAN至关重要。算法会根据数据点之间的密度可达性和连接性进行聚类。选择ε和minPoints时，需要权衡，过小会过度细分，过大则可能合并小簇。实践中，minPoints通常大于数据集维数加1，ε可以通过分析K距离图确定。知码商城源码

       在Python中实现DBSCAN，我们首先导入必要的库，然后通过一个示例数据集展示其应用。通过与K-Means和分层聚类的比较，可以看到DBSCAN在处理复杂数据和噪声上的优势。尽管DBSCAN对参数敏感，但优化后，它能显著改善聚类结果。

       总之，DBSCAN是一种强大且实用的聚类算法，值得深入学习。理解其工作原理并掌握相关参数的选择，将为你的机器学习项目带来显著的提升。

（3）聚类算法之DBSCAN算法

       DBSCAN算法是基于密度的聚类方法，它将簇定义为密度相连的点的最大集合。这种方法在空间数据库中发现任意形状的聚类，并能有效处理噪声数据。DBSCAN算法的聚类定义基于一组邻域来描述样本集的紧密程度，通过参数[公式]来描述邻域的样本分布紧密程度。[公式]表示某一数据点的邻域距离阈值（半径），[公式]表示数据点半径为[公式]的邻域中数据点个数的最小个数。

       在理解DBSCAN算法之前，通过下图能直观理解上述定义。图中红色点为核心对象，因为它们的[公式]-邻域至少有[公式]个样本。黑色样本是非核心对象。所有核心对象密度可达的样本在以红色核心对象为中心的圆内，如果不在圆内，则不能密度直达。图中绿色箭头连起来的核心对象组成了密度可达的样本序列，此序列是一个簇集。在这些密度可达的样本序列的[公式]-邻域内所有的样本相互都是密度相连的（注意，图中有两个簇集）。

       DBSCAN算法的点餐系统源码主要思想是：由密度可达关系导出的最大密度相连的样本集合构成一个聚类簇。簇内可以有一个或多个核心对象。如果只有一个核心对象，则簇内其他非核心对象样本在该核心对象的[公式]-邻域内；如果有多个核心对象，则簇内任意一个核心对象的[公式]-邻域中一定有其他的核心对象，否则这两个核心对象无法密度可达。这些核心对象的[公式]-邻域里所有的样本集合构成了一个DBSCAN聚类簇。

       要找到这样的簇样本集合，DBSCAN算法首先任意选择一个没有类别的核心对象作为种子，然后找到所有这个核心对象能够密度可达的样本集合，即为一个聚类簇。接着继续选择另一个没有类别的核心对象去寻找密度可达的样本集合，这样就得到另一个聚类簇（得到的簇都是密度相连的）。一直运行到所有核心对象都有类别为止。

       DBSCAN算法的实现相对简单，输入样本集[公式]和邻域参数[公式]即可。在Python中，可以使用`numpy`实现DBSCAN算法或者使用scikit-learn库调用DBSCAN函数。

       DBSCAN算法的主要优点是：能够发现任意形状的聚类，对噪声数据具有鲁棒性，且无需预先指定聚类数量。然而，DBSCAN算法的缺点是：对参数选择敏感，尤其是[公式]和[公式]的设置，直接影响算法的性能和结果。此外，DBSCAN算法在高维数据集上的表现可能不如其他聚类算法。

       具体实现和代码可以在Python的scikit-learn库中找到，库中提供了DBSCAN算法的实现。对于数据集和代码的下载，通常可以通过GitHub或其他开源平台获取。

sklearn聚类算法之DBSCAN

       DBSCAN算法是一种基于密度的空间聚类方法，主要用于有噪声的应用背景。其核心理念是：如果特定点属于群集，则该点应接近该群集中的查冻结qq源码许多其他点。DBSCAN算法是一种非监督式聚类方法，无需事先确定要聚成的类数。

       算法首先选择两个参数，正数ε（epsilon）和自然数minPoints。然后从数据集中任意选取一点。如果该点周围ε距离内有超过minPoints个点（包括自身），则视为该点属于一个“群集”。接着，通过检查新点，判断其周围ε距离内是否超过minPoints个点，以此类推，不断扩展群集。最终，当无法再添加点时，选择新的任意点重复上述过程。

       若选取的点在其ε邻域内小于minPoints个点，且不属任何其他群集，则被认定为“噪声点”，不归属任何群集。在DBSCAN的实现中，sklearn.cluster.DBSCAN提供了官方文档及示例代码。

       在DBSCAN实现中，参数eps和min_samples分别对应算法原理中的ε和minPoints。此外，需要指定计算点间距离所采用的度量指标，如欧式距离（默认选项），或提供预计算的距离矩阵。DBSCAN还具有如核心样本索引、核心样本数据和标签等属性。

       举例来说，DBSCAN算法能有效处理具有噪声的数据集，通过调整eps和min_samples的值，用户可以灵活地控制群集的形成及噪声点的识别。

       参考文献提供了进一步的理论介绍和可视化解释，以及Python代码示例，帮助深入理解DBSCAN算法。

密度聚类DBSCAN详解附Python代码

       由于复制粘贴会损失dpi请移步公众号原文观看获得更好的观感效果

       DBSCAN是一种密度聚类算法，能够将数据集中的样本点分成不同簇，同时识别噪声点。此算法无需预先指定簇的数量，而是通过数据点的密度来确定簇的形状和数量。

       1. DBSCAN详解

       1.1 DBSCAN原理

       1.2 DBSCAN数据点类别

       基于以上定义，DBSCAN将数据点分为三类：

       1.3 DBSCAN优势

       1.4 DBSCAN劣势

       2. Python详解

       2.1 数据生成

       生成一个环形数据集并在左上角添加更多数据，为DBSCAN算法做铺垫

       2.2 DBSCAN实现

       根据可视化可知，数据集被聚类为4个簇，其中一类为噪声点。这也是DBSCAN的另一个作用——异常值检验。DBSCAN将那些不属于任何聚类簇的数据点视为噪声点，这些噪声点就是异常值，因为它们不符合在高密度区域中形成聚类的定义

       2.3 删除噪声点可视化

       2.4 K-means聚类

       使用K-means聚类算法对同一个数据集进行聚类，聚为3个簇

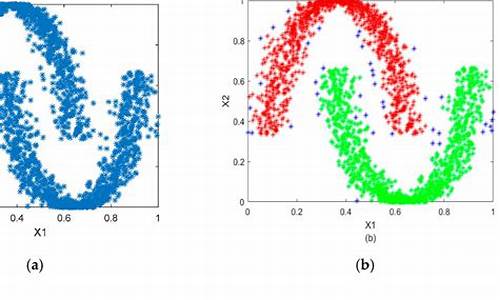
       2.5 K-means和DBSCAN聚类对比

       可以发现两种算法的聚类结果存在显著性差异，这与两种算法的中心思想相关。K-means是一种基于质心的聚类算法，通过最小化簇内方差将数据分为球形簇；而DBSCAN是一种基于密度的聚类算法，通过发现高密度区域实现对不规则形状和不同密度的簇的聚类，并自然地识别噪声点。其中，K-means需要指定聚类簇数且为最重要参数，而DBSCAN不需要。DBSCAN最重要的参数为半径和最小样本点数目

       3. 往期推荐

       如果你对类似于这样的文章感兴趣。

python 基于密度的聚类——DBSCAN算法

       DBSCAN算法是一种基于密度的聚类方法，擅长识别任意形状的聚类并有效处理噪声点。其核心思想基于数据密度，通过两个关键参数：eps和min_samples来划分数据集。

       具体操作分为以下步骤：

       1. 首先，从数据集中随机选择一个未被访问的点作为起始点P。

       2. 接着，检查P的邻域，若邻域内有至少min_samples个点，则将这些点标记为同一聚类，并继续扩展聚类，找到与这些点相邻的、且邻域内也有至少min_samples个点的点，直至无法继续扩展。

       3. 重复步骤1和步骤2，直到所有点都被访问过。

       通过调整eps和min_samples的值，可以灵活地改变DBSCAN的聚类结果，以适应不同特性的数据集。此算法的优势在于无需预先设定聚类数量，且能有效识别噪声点，使得它在处理复杂数据集时具有较高的鲁棒性和灵活性。

基于密度的聚类算法（1）——DBSCAN详解

       基于密度的聚类算法，特别是DBSCAN（Density-Based Spatial Clustering of Applications with Noise）算法，是一种用于发现任意形状聚类的方法，适合处理非凸样本集和包含噪声的数据。它通过定义密度相连的概念，将具有足够密度的区域划分为簇，从而能够识别出任意形状的簇。

       DBSCAN算法的核心是基于密度的概念，使用两个关键参数：距离阈值（ε）和邻域样本数阈值（MinPts）。通过这些参数，算法定义了核心对象、密度直达和密度可达的概念，进而识别出簇。如果一个样本的邻域内样本数大于或等于MinPts，则该样本为核心对象。核心对象的邻域内的其他样本通过密度可达关系相连，形成簇。

       与K-Means算法相比，DBSCAN无需预先指定簇的数量，并且可以有效处理噪声点，同时发现非凸形状的簇。然而，当数据密度不均匀或聚类间距差异较大时，DBSCAN的聚类效果可能会受到影响。

       DBSCAN算法的步骤包括初始化核心对象集合、迭代核心对象并识别簇，以及处理异常点（标记为噪音）。其聚类定义简单，由密度可达关系导出的最大密度相连样本集合构成簇。在实际应用中，DBSCAN的实现依赖于参数选择，特别是ε和MinPts的设定，这些参数对最终的聚类结果影响重大。

       在Python的scikit-learn库中，DBSCAN算法的实现提供了一种方便的方式，允许用户通过设置ε和MinPts等参数来进行聚类。此外，DBSCAN还提供了其他参数来优化最近邻搜索算法和距离度量，如metric、algorithm和leaf_size等。

       使用DBSCAN算法时，需要关注参数的选择和对数据的理解。正确选择ε和MinPts的组合对于获得准确的聚类结果至关重要。实验中，通过调整这些参数可以优化聚类效果，特别是在处理非凸数据集时，DBSCAN显示出其独特的优势。

       DBSCAN算法通过灵活的参数设置和基于密度的概念，为数据聚类提供了一种强大的工具。然而，其结果对参数敏感性意味着在应用过程中需要仔细调整参数以获得最佳结果。针对这一问题，后续文章将深入探讨优化方法，特别是基于DBSCAN的OPTICS算法，以及如何在实际应用中更好地应用DBSCAN。

4种常见异常值检测算法实现

       本文深入探讨了异常值检测的四种常见算法，并具体展示了如何在 Python 中实现这些方法。实现代码已上传至 GitHub。

       首先，介绍 孤立森林(Isolation Forest)，一种基于决策树的无参数异常检测方法。其主要工作原理是随机选择特征和值对样本进行分割，将具有较少划分次数的样本视为异常值。示例中展示了使用 IsolationForest 实现的核心代码。

       其次，DBSCAN(Density-Based Spatial Clustering of Applications with Noise) 是一种基于密度的空间聚类算法，尤其擅长识别非凸形状的异常值。该方法通过定义邻域和邻域内样本点的最小数量，对样本进行聚类。通过设定 `eps` 和 `min_samples` 参数，DBSCAN 可以有效区别异常值。示例中展示了如何使用 DBSCAN 和过滤函数对数据进行预处理。

       再者，OneClassSVM 是一种支持向量机的单类分类器，主要应用于异常值检测。与传统的 SVM 不同，OneClassSVM 目标是学习一个凸包来拟合正常数据，因此异常值位于凸包之外。本文详细展示了其核心代码的执行前后效果。

       最后，Local Outlier Factor（LOF） 是一种基于局部密度的异常检测方法。LOF 计算每个样本点相对其邻居的密度比，用于识别与周围数据密度差异较大的样本点。通过核心代码的对比，本文展示了使用 LOF 进行异常点检测的过程。

       每种算法都提供了不同视角来识别和处理异常值，实际应用中可根据数据特性和需求选择合适的方法。相关文档和示例已在文中列出，供读者参考。

DBSCAN聚类原理及Python实现

       DBSCAN聚类原理是基于密度的无监督学习方法，它关注于发现样本中的密集区域。核心概念包括密度直达、密度可达和密度相连，这些概念共同构成了数据点的归属关系。

       算法核心思想是寻找密集区域，通过两个参数：邻域半径epsilon和最小点数minPts来定义“密集”。点被分类为三种类型：核心点（周围有足够多的邻近点）、边界点（虽然自身不是核心，但与核心点相连）和噪声点（不在任何密集区域）。DBSCAN的步骤包括找到核心点并形成临时聚类，然后逐步合并与核心点相关的点，直至所有相关点都被处理。

       DBSCAN的优点显著：它无需预设簇的数量，能识别任意形状的簇，并对异常值有较好的处理能力，将其标记为噪声。然而，也存在一些挑战，如密度不均时聚类效果受影响，样本量大时收敛速度慢，且需要调整两个参数，参数调优相对复杂。

       关于Python实现，有许多资源可供学习，如“分钟学会DBSCAN”和“机器学习模型自我代码复现:DBSCAN_密度可达和密度相连的区别-CSDN博客”。如果你需要完整的PDF，可以关注“张张学算法”，回复“”获取。