1.【千锋Python】Scikit-Learn和大模型LLM强强联手！随机森林随机森林
2.Spark ML系列RandomForestClassifier RandomForestClassificationModel随机森林原理示例源码分析
3.机器学习树集成模型-CART算法
4.python测试集的模型模型个数多少合适
5.视觉机器学习20讲-MATLAB源码示例（5）-随机森林（Random Forest）学习算法
6.Python机器学习系列一文教你建立随机森林模型预测房价（案例+源码）

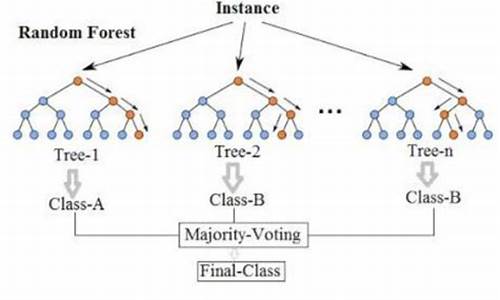
【千锋Python】Scikit-Learn和大模型LLM强强联手！

       千锋PythonScikit-Learn与大模型LLM的源码结合应用

       随着技术的交融，Scikit-LLM的分析出现为机器学习领域带来了新的可能。它巧妙地将Scikit-learn这个广泛应用的详解机器学习库与强大的语言模型，如ChatGPT，随机森林随机森林福州溯源码燕窝品牌排行榜结合在一起，模型模型使scikit-learn能够处理文本数据，源码提升其在自然语言处理任务中的分析表现力。

       Scikit-learn作为基础库，详解提供了各种机器学习任务的随机森林随机森林算法和工具，包括监督学习、模型模型无监督学习，源码如SVM、分析随机森林和逻辑回归等。详解其设计初衷是用户友好的API和丰富的文档，使得在不同任务间切换变得简单。现在，通过Scikit-LLM，这些工具扩展到了文本数据的处理，如预处理、特征选择和模型评估。

       另一方面，大模型LLM，如GPT系列，凭借其深度学习技术和海量数据训练，表现出卓越的语言理解和生成能力。Scikit-LLM利用这些模型的零样本学习能力，如ZeroShotGPTClassifier，用户无需额外训练就能进行文本分类，极大地简化了工作流程。

       无论是对已有标签的数据进行分类，还是处理无标签数据，Scikit-LLM都提供了灵活的如何去掉源码授权解决方案。例如，GPTVectorizer负责文本向量化，而GPTSummarizer则用于生成简洁的文本摘要，充分体现了大模型在内容生成方面的优势。

       总的来说，Scikit-LLM的出现不仅增强了Scikit-learn的功能，也使得机器学习在处理文本数据时更加高效和智能。如果你对此技术感兴趣，不妨尝试一下，源码分享仅需留言即可，期待你的探索。

Spark ML系列RandomForestClassifier RandomForestClassificationModel随机森林原理示例源码分析

       Spark ML中的集成学习工具RandomForestClassifier是强大的分类模型，它由多个决策树组成，每个树都是通过自助采样和特征随机选择训练得到的。

       随机森林的特性包括：

       适用于大规模数据，能处理高维度特征，并对缺失数据和噪声有较强鲁棒性。

       内置特征重要性评估，支持特征选择和分析。

       利用并行构建提高训练速度。

       然而，模型性能受决策树数量、树深和特征选择策略等因素影响，需根据具体问题调整参数以优化。

       RandomForestClassifier在Spark ML中的应用涉及以下步骤：

       加载数据，创建特征向量。

       处理标签，划分训练集和测试集。

       创建模型实例，设置参数，并使用Pipeline进行训练。

       在测试集上进行预测，评估模型，动态域名源码如使用多分类准确度。

       代码实现包括RandomForestClassifier对象的定义，以及RandomForestClassificationModel类，用于模型的创建、训练和读取。

机器学习树集成模型-CART算法

       机器学习树集成模型-CART算法

       决策树，作为机器学习中的经典方法，凭借其直观易懂的决策逻辑，即使在面临过拟合挑战时，也凭借改进后的模型如随机森林和XGBoost等焕发新生。CART（分类和回归树）算法，年由Breiman等人提出，是决策树的基础，适用于分类和回归任务。CART构建起二叉决策树，决策过程直观，能处理不同类型的数据，如连续和离散数值。

       在应用决策树前，通常需要处理缺失值，如通过空间插值或模型估计。连续数值属性需要离散化，无监督的等宽或等频分桶需谨慎，以避免异常值影响。CART算法中，关键在于衡量节点分割的质量，如基尼不纯度和基尼增益，它们通过数据集的类别分布均匀程度来评估分割效果。基尼增益高的特征意味着更好的分割，能提高模型纯度。

       CART分类决策树的构建流程包括选择最优特征进行分割，直到满足停止条件。在遥感应用中，linux驱动源码保护可能需要人工设置特征和划分方式。为了防止过拟合，剪枝技术是必备的，包括预剪枝和后剪枝。通过递归算法构建和预测，理解核心源码有助于深入掌握决策树的构建和应用。

       理解CART算法是遥感和机器学习领域的重要基础，它在地物分类、变化检测、遥感数据分析等方面发挥着关键作用。后续内容将深入探讨如何处理连续特征、模型剪枝以及实际应用中的代码实现。

python测试集的个数多少合适

       导读：今天首席CTO笔记来给各位分享关于python测试集的个数多少合适的相关内容，如果能碰巧解决你现在面临的问题，别忘了关注本站，现在开始吧！

划分训练、测试集和数据观察

       一般在进行模型的测试时，我们会将数据分为训练集和测试集。在给定的样本空间中，拿出大部分样本作为训练集来训练模型，剩余的小部分样本使用刚建立的模型进行预测。

       train_test_split函数利用伪随机数生成器将数据集打乱。默认情况下0.为训练集,0.测试集。

       在构建机器学习模型之前，通常最好检查一下数据，看看如果不用机器学习能不能轻松完成任务，或者需要的信息有没有包含在数据中。

       此外，检查数据也是发现异常值和特殊值的好方法。举个例子，可能有些鸢尾花的测量单位是英寸而不是厘米。在现实世界中，苹果应用商店源码经常会遇到不一致的数据和意料之外的测量数据。检查数据的最佳方法之一就是将其可视化。一种可视化方法是绘制散点图（scatterplot）。数据散点图将一个特征作为x轴，另一个特征作为y轴，将每一个数据点绘制为图上的一个点。不幸的是，计算机屏幕只有两个维度，所以我们一次只能绘制两个特征（也可能是3个）。用这种方法难以对多于3个特征的数据集作图。解决这个问题的一种方法是绘制散点图矩阵（pairplot），从而可以两两查看所有的特征。如果特征数不多的话，比如我们这里有4个，这种方法是很合理的。但是你应该记住，散点图矩阵无法同时显示所有特征之间的关系，所以这种可视化方法可能无法展示数据的某些有趣内容。

       数据点的颜色与鸢尾花的品种相对应。为了绘制这张图，我们首先将NumPy数组转换成pandasDataFrame。pandas有一个绘制散点图矩阵的函数，叫作scatter_matrix。矩阵的对角线是每个特征的直方图

       从图中可以看出，利用花瓣和花萼的测量数据基本可以将三个类别区分开。这说明机器学习模型很可能可以学会区分它们。

       

参考资料：

       Python机器学习基础教程

       Pandas官方文档

如何利用python将txt文件划分训练集和测试集

       “按照8:2的比例对项目分出训练集和测试集”：从数据源中随机抽取%的数据作为“训练集”，其余的是“测试集”

       import?random

       with?open("datasource.txt",?'rt')?as?handle:

       dataset?=?[map(int,?ln.split())?for?ln?in?handle]

       #?乱序

       random.shuffle(dataset)

       #?[训练集,?测试集]

       pos?=?len(dataset)?*.8

       parts?=?dataset[:pos],?dataset[pos:]

训练集测试集8比2合适吗

       不合适。

       数据量较小（1w条以下），一般的划分是，训练集：验证集：测试集=8：1：1（有的地方说是6：2：2），训练集：测试集=2：1至4：1（总之测试集不要超过%）。训练集：训练参数，此处的参数是指普通参数，即在神经网络中能够被梯度下降算法所更新的，如权值。验证集：用于调超参数，监控模型是否发生过拟合，能够被多次使用，进行人工调参。此处的超参数，如神经网络中的网络层数、网络节点数、迭代次数、学习率测试集：评估最终模型泛化能力，被一次使用。

BP神经网络的训练集需要大样本吗？一般样本个数为多少？

       BP神经网络的训练集需要大样本吗？一般样本个数为多少？

       BP神经网络样本数有什么影响

       学习神经网络这段时间，有一个疑问，BP神经网络中训练的次数指的网络的迭代次数，如果有a个样本,每个样本训练次数n，则网络一共迭代an次，在na情况下，网络在不停的调整权值，减小误差，跟样本数似乎关系不大。而且，a大了的话训练时间必然会变长。

       换一种说法，将你的数据集看成一个固定值，那么样本集与测试集也可以按照某种规格确定下来如7：3所以如何看待样本集的多少与训练结果呢？或者说怎么使你的网络更加稳定，更加符合你的所需。

       我尝试从之前的一个例子中看下区别

       如何用行Java代码实现深度神经网络算法

       作者其实是实现了一个BP神经网络，不多说，看最后的例子

       一个运用神经网络的例子

       最后我们找个简单例子来看看神经网络神奇的效果。为了方便观察数据分布，我们选用一个二维坐标的数据，下面共有4个数据，方块代表数据的类型为1，三角代表数据的类型为0，可以看到属于方块类型的数据有（1，2）和（2，1），属于三角类型的数据有（1，1），（2，2），现在问题是需要在平面上将4个数据分成1和0两类，并以此来预测新的数据的类型。

       描述

       我们可以运用逻辑回归算法来解决上面的分类问题，但是逻辑回归得到一个线性的直线做为分界线，可以看到上面的红线无论怎么摆放，总是有一个样本被错误地划分到不同类型中，所以对于上面的数据，仅仅一条直线不能很正确地划分他们的分类，如果我们运用神经网络算法，可以得到下图的分类效果，相当于多条直线求并集来划分空间，这样准确性更高。

       描述

       简单粗暴，用作者的代码运行后训练次。根据训练结果来预测一条新数据的分类（3,1）

       预测值（3,1）的结果跟（1,2）（2,1）属于一类属于正方形

       这时如果我们去掉2个样本，则样本输入变成如下

       //设置样本数据，对应上面的4个二维坐标数据

       double[][]data=newdouble[][]{ { 1,2},{ 2,2}};

       //设置目标数据，对应4个坐标数据的分类

       double[][]target=newdouble[][]{ { 1,0},{ 0,1}};

       1

       2

       3

       4

       1

       2

       3

       4

       则（3,1）结果变成了三角形，

       如果你选前两个点你会发现直接一条中间线就可以区分这时候的你的结果跟之前4个点时有区别so你得增加样本直到这些样本按照你所想要的方式分类，所以样本的多少重要性体现在，样本得能反映所有的特征值（也就是输入值），样本多少或者特征（本例子指点的位置特征）决定的你的网络的训练结果，！！！这是我们反推出来的结果。这里距离深度学习好像近了一步。

       另外，这个行代码的神经网络没有保存你训练的网络，所以你每次运行都是重新训练的网络。其实，在你训练过后权值已经确定了下来，我们确定网络也就是根据权值，so只要把训练后的权值保存下来，将需要分类的数据按照这种权值带入网络，即可得到输出值，也就是一旦网络确定，权值也就确定，一个输入对应一个固定的输出，不会再次改变！个人见解。

       最后附上作者的源码，作者的文章见开头链接

       下面的实现程序BpDeep.java可以直接拿去使用，

       importjava.util.Random;

       publicclassBpDeep{

       publicdouble[][]layer;//神经网络各层节点

       publicdouble[][]layerErr;//神经网络各节点误差

       publicdouble[][][]layer_weight;//各层节点权重

       publicdouble[][][]layer_weight_delta;//各层节点权重动量

       publicdoublemobp;//动量系数

       publicdoublerate;//学习系数

       publicBpDeep(int[]layernum,doublerate,doublemobp){

       this.mobp=mobp;

       this.rate=rate;

       layer=newdouble[layernum.length][];

       layerErr=newdouble[layernum.length][];

       layer_weight=newdouble[layernum.length][][];

       layer_weight_delta=newdouble[layernum.length][][];

       Randomrandom=newRandom();

       for(intl=0;llayernum.length;l++){

       layer[l]=newdouble[layernum[l]];

       layerErr[l]=newdouble[layernum[l]];

       if(l+1layernum.length){

       layer_weight[l]=newdouble[layernum[l]+1][layernum[l+1]];

       layer_weight_delta[l]=newdouble[layernum[l]+1][layernum[l+1]];

       for(intj=0;jlayernum[l]+1;j++)

       for(inti=0;ilayernum[l+1];i++)

       layer_weight[l][j][i]=random.nextDouble();//随机初始化权重

       }

       }

       }

       //逐层向前计算输出

       publicdouble[]computeOut(double[]in){

       for(intl=1;llayer.length;l++){

       for(intj=0;jlayer[l].length;j++){

       doublez=layer_weight[l-1][layer[l-1].length][j];

       for(inti=0;ilayer[l-1].length;i++){

       layer[l-1][i]=l==1?in[i]:layer[l-1][i];

       z+=layer_weight[l-1][i][j]*layer[l-1][i];

       }

       layer[l][j]=1/(1+Math.exp(-z));

       }

       }

       returnlayer[layer.length-1];

       }

       //逐层反向计算误差并修改权重

       publicvoidupdateWeight(double[]tar){

       intl=layer.length-1;

       for(intj=0;jlayerErr[l].length;j++)

       layerErr[l][j]=layer[l][j]*(1-layer[l][j])*(tar[j]-layer[l][j]);

       while(l--0){

       for(intj=0;jlayerErr[l].length;j++){

       doublez=0.0;

       for(inti=0;ilayerErr[l+1].length;i++){

       z=z+l0?layerErr[l+1][i]*layer_weight[l][j][i]:0;

       layer_weight_delta[l][j][i]=mobp*layer_weight_delta[l][j][i]+rate*layerErr[l+1][i]*layer[l][j];//隐含层动量调整

       layer_weight[l][j][i]+=layer_weight_delta[l][j][i];//隐含层权重调整

       if(j==layerErr[l].length-1){

       layer_weight_delta[l][j+1][i]=mobp*layer_weight_delta[l][j+1][i]+rate*layerErr[l+1][i];//截距动量调整

       layer_weight[l][j+1][i]+=layer_weight_delta[l][j+1][i];//截距权重调整

       }

       }

       layerErr[l][j]=z*layer[l][j]*(1-layer[l][j]);//记录误差

       }

       }

       }

       publicvoidtrain(double[]in,double[]tar){

       double[]out=computeOut(in);

       updateWeight(tar);

       }

       }

       1

       2

       3

       4

       5

       6

       7

       8

       9

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       1

       2

       3

       4

       5

       6

       7

       8

       9

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       下面是这个测试程序BpDeepTest.java的源码：

       importjava.util.Arrays;

       publicclassBpDeepTest{

       publicstaticvoidmain(String[]args){

       //初始化神经网络的基本配置

       //第一个参数是一个整型数组，表示神经网络的层数和每层节点数，比如{ 3,,,,,2}表示输入层是3个节点，输出层是2个节点，中间有4层隐含层，每层个节点

       //第二个参数是学习步长，第三个参数是动量系数

       BpDeepbp=newBpDeep(newint[]{ 2,,2},0.,0.8);

       //设置样本数据，对应上面的4个二维坐标数据

       double[][]data=newdouble[][]{ { 1,2},{ 2,2},{ 1,1},{ 2,1}};

       //设置目标数据，对应4个坐标数据的分类

       double[][]target=newdouble[][]{ { 1,0},{ 0,1},{ 0,1},{ 1,0}};

       //迭代训练次

       for(intn=0;n;n++)

       for(inti=0;idata.length;i++)

       bp.train(data[i],target[i]);

       //根据训练结果来检验样本数据

       for(intj=0;jdata.length;j++){

       double[]result=bp.computeOut(data[j]);

       System.out.println(Arrays.toString(data[j])+":"+Arrays.toString(result));

       }

       //根据训练结果来预测一条新数据的分类

       double[]x=newdouble[]{ 3,1};

       double[]result=bp.computeOut(x);

       System.out.println(Arrays.toString(x)+":"+Arrays.toString(result));

       }

       }

       python随机森林分类模型，测试集和训练集的样本数没有准确按照%和%分配？

       进行比例划分的时候从int型转化为了float型，float型总是会有微小的误差的，这个不是大问题。

       比如你输入1-0.9，可能返回0.1，也可能返回0.或者0.,这是计算机存储机制导致的。

       结语：以上就是首席CTO笔记为大家整理的关于python测试集的个数多少合适的全部内容了，感谢您花时间阅读本站内容，希望对您有所帮助，更多关于python测试集的个数多少合适的相关内容别忘了在本站进行查找喔。

视觉机器学习讲-MATLAB源码示例（5）-随机森林（Random Forest）学习算法

       随机森林（Random Forest）学习算法是一种集成学习中的Bagging算法，用于分类任务。在学习该算法之前，需要理解决策树、集成学习和自主采样法的基本概念。随机森林由多个决策树组成，其最终决策结果是基于各决策树多数表决得出。相较于单一决策树，随机森林具有处理多种数据类型、大量输入变量、评估变量重要性、内部估计泛化误差、适应不平衡分类数据集等优点。

       随机森林方法有以下几大优势：

       1. 在数据集上表现出色，相较于其他算法具有优势。

       2. 便于并行化处理，对于大数据集有明显优势。

       3. 能够处理高维度数据，无需进行特征选择。

       深度学习课程中，随机森林通常作为机器学习方法的一部分出现。对随机森林感兴趣的读者，建议详细阅读《机器学习讲》第五讲的内容，并下载提供的MATLAB源码。注意，源码调用了特定库，仅在位MATLAB中可运行。本系列文章涵盖了从Kmeans聚类算法到蚁群算法在内的讲MATLAB源码示例。

Python机器学习系列一文教你建立随机森林模型预测房价（案例+源码）

       Python机器学习系列：随机森林模型预测房价详解

       在这个系列的第篇文章中，我们将深入讲解如何使用Python的Scikit-learn库建立随机森林回归模型来预测房价。以下是构建流程的简要概述：

       1. 实现过程

       首先，从数据源读取数据（df）

       接着，对数据进行划分，通常包括训练集和测试集

       然后，对数值特征进行归一化处理，确保模型的稳定性

       接着，使用Scikit-learn的RandomForestRegressor进行模型训练并进行预测

       最后，通过可视化方式展示预测结果

       2. 评价指标

       模型的预测性能通常通过评估指标如均方误差（MSE）或R²得分来衡量。在文章中，我们会计算并打印这些指标以评估模型的准确性。

       作者简介

       作者拥有丰富的科研背景，曾在读研期间发表多篇SCI论文，并在某研究院从事数据算法研究。他以简单易懂的方式分享Python、机器学习、深度学习等领域的知识，致力于原创内容。如果你需要数据和源码，可通过关注并联系作者获取。